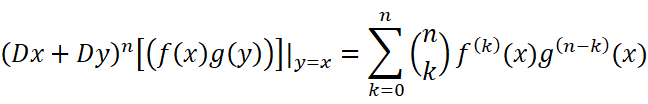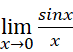-
【高数学习回顾】6.筑基导数应用的大厦:拥抱拉格朗日中值定理
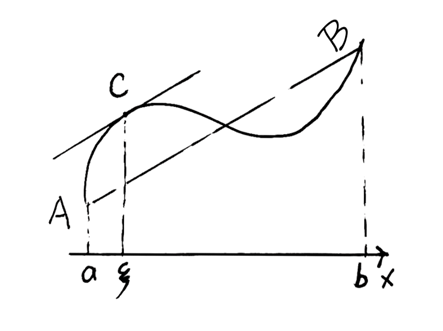
我们观察一个不符合罗尔定理条件的函数,然后稍稍把它旋转一下…这不就回到罗尔定理了嘛!
-
【高数学习回顾】5.筑基导数应用的大厦:从费马引理和罗尔定理聊起
正如标题所言,接下来几篇小文会回顾导数应用大厦底层的建立。这个系列会从费马引理和罗尔定理聊起,进而推导出拉格朗日中值定理,进而推导出柯西中值定理。然后,得到十分常用的洛必达定理。最后,得到泰勒公式和麦克劳林展开式。我认为…
-
【高数学习回顾】4.莱布尼茨公式,但是二项式定理
这个证明方式优美得就像….呃,人体曲线?毕竟二者都具有对称的美感(虽然我也觉得这个比喻很离谱)。但其实也并非完全一致,曲线是直接呈现出来的对称,而二项式定理和莱布尼茨公式间是潜藏但是能直观感受到的一种对称。
-
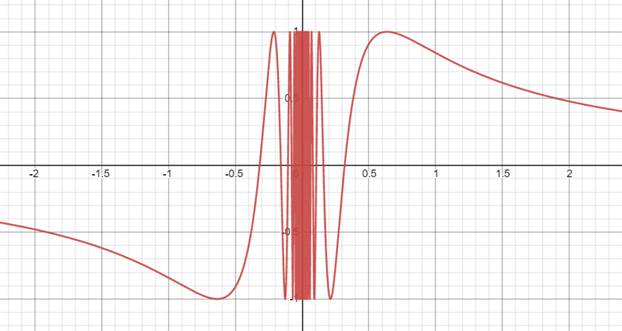
【高数学习回顾】3.渐近线的爱恨情仇
高中时的数学老师特别喜欢开渐近线的玩笑:“无限接近,永不相交”,用来比喻某种爱而不得的感情状态。除此之外,时不时也能看到夜半网易云语录里出现渐近线的身影,类似“还是渐近线好,真要相交只能以后渐行渐远”,“你始终是我触碰不…
-
【高数学习回顾】2.函数的连续性与间断点
判断连续和间断点并不是一件复杂的事情。在我刚开始学习高数时,判断连续系列的问题经常让我痛不欲生。不过等到稍稍往后学习后,这类问题已经再也难不倒我了!不过我很怀念,彼时彼刻,我用着最最基础的数学工具思考函数连续时的样子。
-
我的摄影代表作
我的摄影代表作:回望过去,展望未来。甄选了能代表我摄影生涯的一些照片。摄影是对周遭的观察,生活中到处都是照片,问题在于能否注意到,并将这些画面组织起来。你需要时刻关注四周,注意那些充满人性以及喜悦的画面。
-
【高数学习回顾】1.为什么要引入第一个重要极限
第一个重要极限它并没有它看上去那么蠢。它可以建立三角函数的微分体系。
-
【物理发展】1.“波粒二象性”是如何一步步建立的?
“物理学的大厦已经基本建成了,后辈物理学家只要做一些零碎的修补工作就行了”,在世纪之交1900年时,威廉·汤姆森发表了这一次异常著名的演讲,“不过在物理学阳光灿烂的天空下,漂浮着两朵小乌云。”开尔文男爵的想法也代表了当时…
-
【随处可见的物理】2.交流电的有效值是什么?
交流电的大小和方向是变化的,这导致电路中的测量和计算有诸多不便。有没有一种办法,可以便捷地表示交流电的特性呢?于是我找来一个奇妙的电水壶,假装在里面灌满水,用家里的电源开始加热它。一段时间后水开了,记录下烧开一壶水所需时…
-
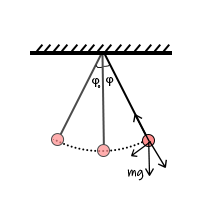
【随处可见的物理】1. 单摆的周期到底是啥?
话说十六世纪的比萨的一天,跟我差不多年龄的伽利略在礼拜时摸鱼,盯着教堂顶的大吊灯发呆。最开始工人不小心触动了吊灯,吊灯的摆动幅度很大,随着时间流逝,摆动幅度也就越来越小。可是,似乎无论摆动幅度是多大,吊灯来回摆动一次的时…