【高数学习回顾】13.定积分的几何应用：弧长、面积和体积

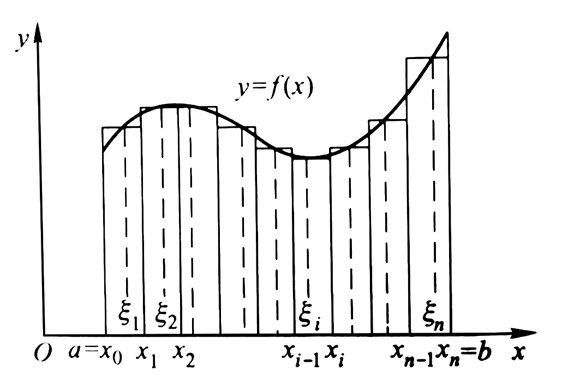
如果大家还记得定积分这个运算是如何定义的（见《12.走进定积分：积分上限的函数和牛顿-莱布尼茨公式》），那定积分可以用来求面积就显而易见了：

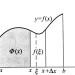
我们来研究一下这两条曲线围成部分的面积：

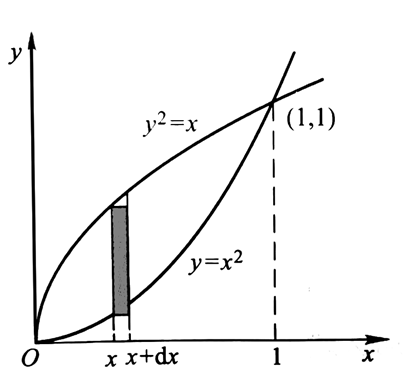
在一段极小段区间[x,x+dx]上，把面积A的增加量可以看作一个长方形，长方形的宽是dx，高是两函数之差。所以我们可以得到：

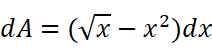
在两交点之间的区间[0,1]上作定积分就可以求得A：

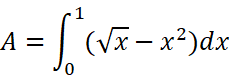
我们只能用x作为积分变量吗？显然不是的。我们再来研究一下这两条曲线围成部分的面积：

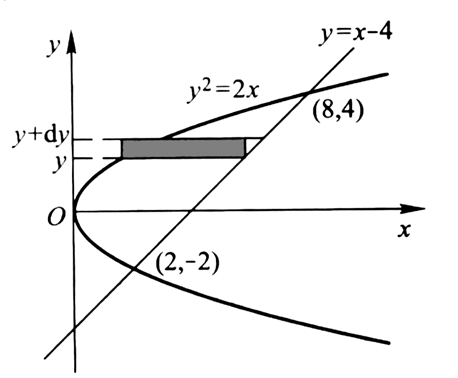
这时选取x作为积分变量会很不方便：即需要把面积分成两部分再分别计算。这时我们可以考虑用y当做积分变量。一样的思路，在一段极小段区间[y,y+dy]上，把面积A的增加量可以看作一个长方形，长方形的宽是两函数x值的差，高是dy。所以我们可以得到：

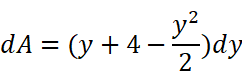
在两交点之间的y区间[-2,4]上作定积分就可以求得A：

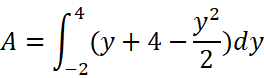
总结二者，我们需要找到的是面积增量与x或y的增量的关系：

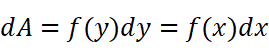
然后在需要的区间上作定积分：

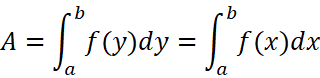
有时直接化出f(x)或f(y)可能不方便，我们也可以考虑使用参数方程，如求椭圆的面积：

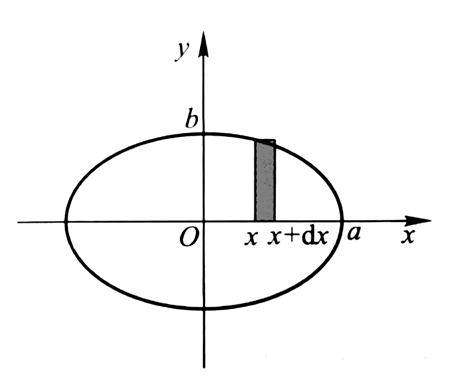
根据对称性，我们只需要求得第一象限的面积A1，乘以4就可以得到椭圆面积A：

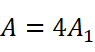
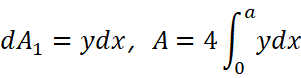
利用椭圆的参数方程：

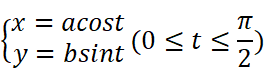
求解方程：

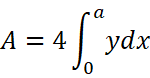
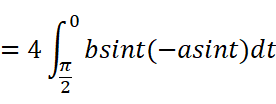
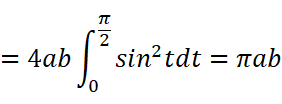
当a=b时，可以顺便得到圆的面积公式：

对于另外一些平面图形，相比用方程，使用极坐标来描述会简单很多。所以我们再来研究一下在极坐标中如何计算。

这时我们可以把面积看作无数个小扇形组成，要考虑的小区间变为了[θ, θ+dθ]，即扇形的圆心角。扇形的边长就是极径ρ。所以面积的增量可以表示为：

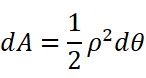
然后在需要的区间上积分，就求得了面积A：

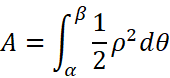
核心思想依然是找到两个增量之间的关系。

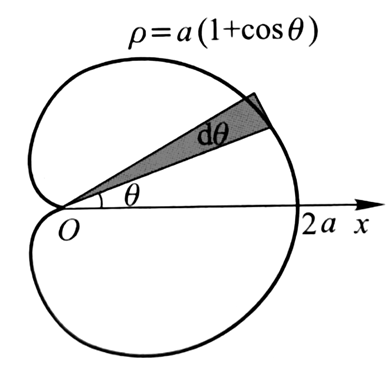
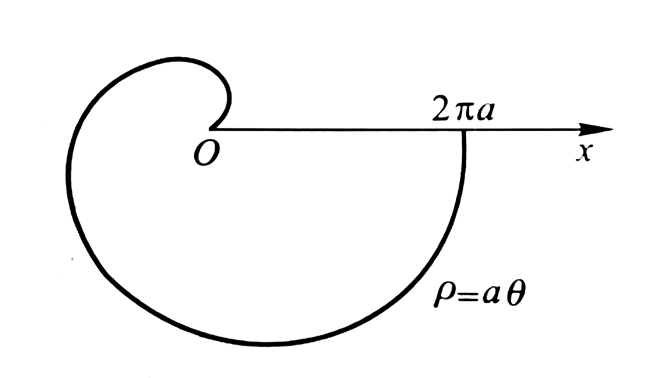
举个例子，我们来看看著名的阿基米德螺线：

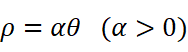
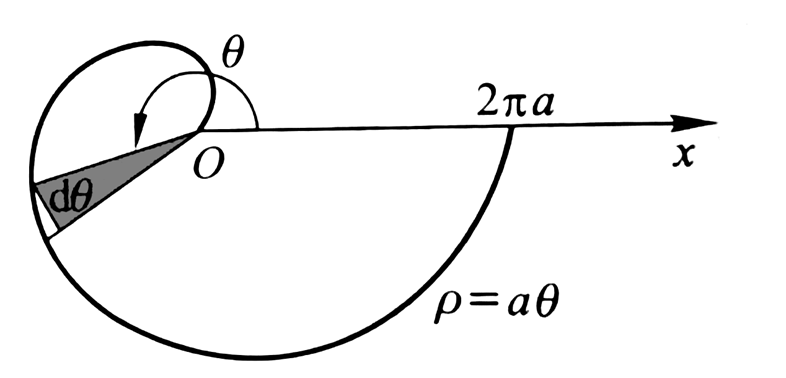
它与极轴所围成的面积的增量是：

所以所求面积为：

试图留下一些习题(解析…真的需要吗)：

T1. 求阴影部分面积：

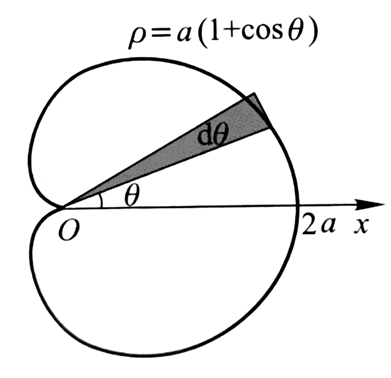
T2. 计算心形线所围成的图形的面积：

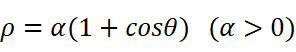
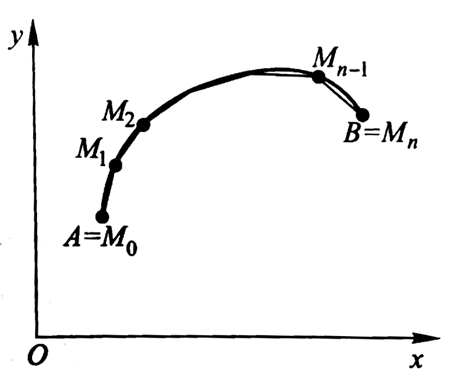
我们已经讨论完了如何用定积分求平面图形的面积。自然而然，我们会想到“升维”或者“降维”。那就从降维开始，研究一下如何求出曲线的长度吧。

我们曾经证明过弧微分（参考《11.导数应用的实例：曲率到底是什么？》，这里仅简单说明）：即用直角三角形的斜边拟合一段极短的曲线.

对于参数方程：

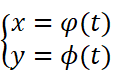
可以得到：

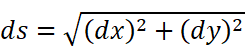
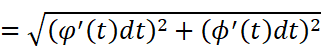
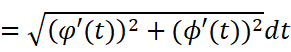
咦，这不就是s的增量与另外的增量的关系嘛。我们在对于区间上作定积分：

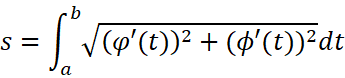
这就是弧长的计算公式。当我们用直角坐标表示时，即：

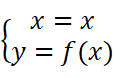
所以：

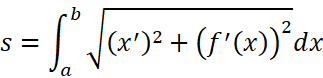
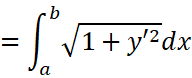
对于极坐标方程

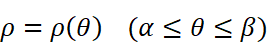
也是同理：

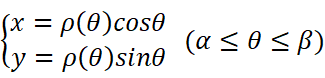
所以：

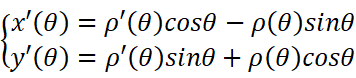
得：

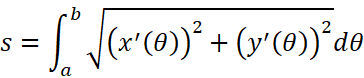
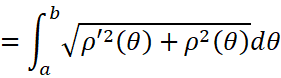
接下来就可以愉快地看几种常见的情况啦：

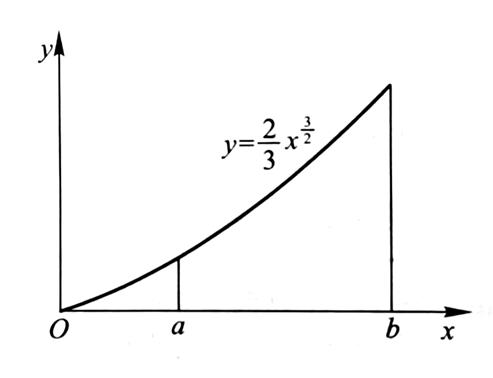
首先是最简单的直角坐标。[a,b]那段弧的长度s为：

然后是参数方程形式的摆线，我们求一下它在0到2πa间的弧长：

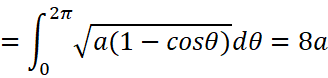
最后是我们刚研究完面积的阿基米德螺线，我们来求一下它的总长：

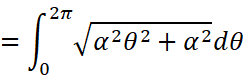
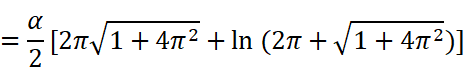
再次试图留两个习题：

T3. 和T2照应一下，计算心形线的全长：

T4. 求圆的渐伸线（如图），当t在0到2π之间的一段弧的长度：

聊完了降维，现在该轮到升维了：应用定积分求体积。

首先是旋转体。旋转体包括圆柱，圆台，圆锥，球等，是由某个图形绕某条轴线旋转一周形成的立体图形。我们还是运用找到两个增量之间的关系这个思想：

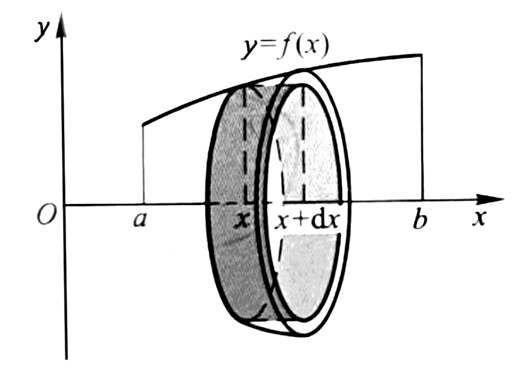
可以把旋转体看作无数个高为dx的圆台的组合，圆台的半径就是f(x)，那么体积的增量dV可以表示为：

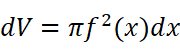
在区间上作定积分：

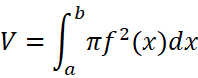
我们来看一个实例：计算椭圆绕x轴一周形成的旋转体（即旋转椭球体）的体积：

它也可以看作是半个椭圆

旋转一周形成的立体。根据我们刚刚的思想，很容易得到：

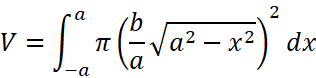
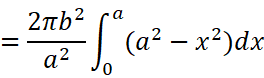
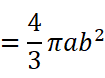
顺便也能得到球的体积计算公式：

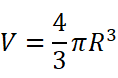
作为推广，若想求体积的形状不是旋转体时，如果我们能知道每个截面的面积，依然可以用同样的思路求出体积：

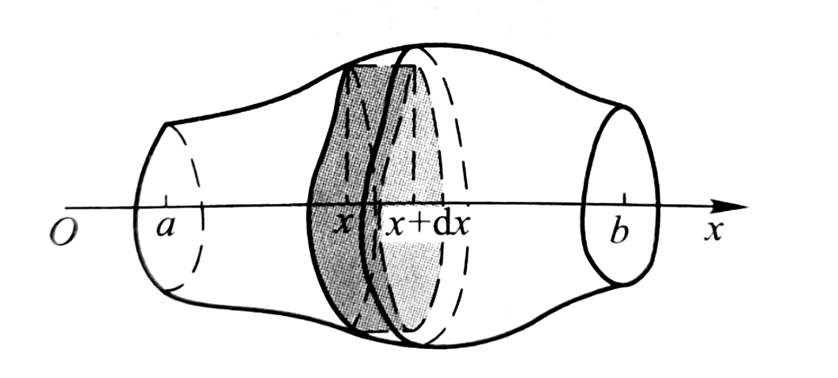
设截面的面积为A(x)，把整个形状看成无数个“台”组成，那么体积的增量为：

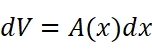
所以体积V就为:

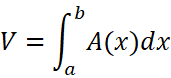
我们再来看一个实例：找一个足够高的圆台，过底部的圆的原因用一个平面截这个圆台，求截得的部分的体积：

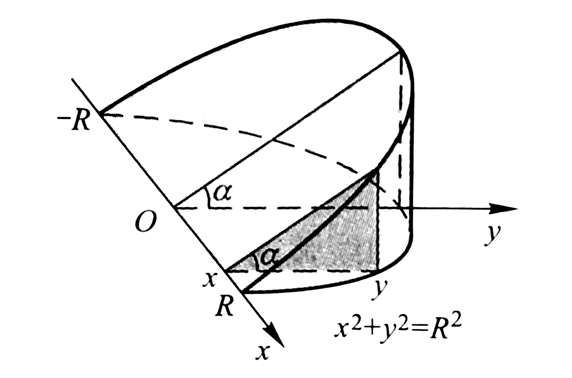
截面是一个直角三角形，两个直角边的长度分别为y和ytana，所以截面面积为：

于是定积分就可以得到体积：

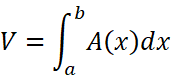
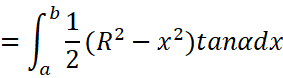
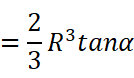
最后仍然再次试图留下习题：

T5. 星形线：

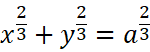
它绕x轴旋转一周会得到一个很优美的图形。求它的体积。

T6. 有如图所示的底面为圆的一个图形，所有垂直于某条直径的截面都是正三角形。求它的体积：