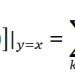正如标题所言，接下来几篇小文会回顾导数应用大厦底层的建立。这个系列会从费马引理和罗尔定理聊起，进而推导出拉格朗日中值定理，进而推导出柯西中值定理。然后，得到十分常用的洛必达定理。最后，得到泰勒公式和麦克劳林展开式。我认为这些内容可以组成“导数应用大厦”的地基了。

我们从费马引理开始，慢慢理清这一大堆内容吧。

史诗的前传：费马引理

先来看看费马引理的内容：

设函数在点x0的某邻域U0(x0)内有定义，并在x0处可导，若

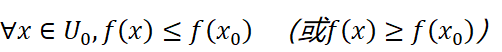
那么

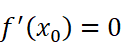
把这个导数为零的点称为驻点

费马引理的证明是非常容易的，我们快速通过：

不妨设

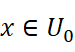
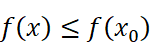
对于

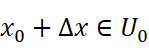
，有：

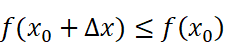
分别考虑左右导数：

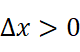
时，

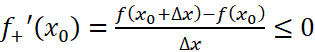
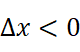
时，

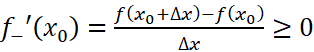
根据可导的条件：

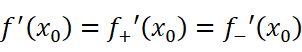
所以得到：

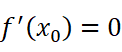
证毕。费马引理解释了函数的一个重要特性：极值点。（注：极值点并不一定是驻点，如y=abs(x)）。我无法太多描述费马引理意味着什么，但是他的意义可以在后续内容中探索：它给罗尔定理的证明打下了基础，敬请见证：

注：为了简化描述，后续我在陈述三大微分中值定理时会省略掉这两个条件：

在闭区间[a,b]上连续

在开区间(a,b)上可导

但这两个条件绝对不能忽略。后续我会深入讨论这两个条件的意义。

打开新世界的大门：罗尔定理

罗尔定理的内容：

若

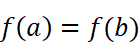
则

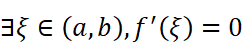
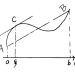
从几何意义上考虑，即至少能找到一个点与x轴平行：

简单证明一下：

由于f(x)在[a,b]上连续，所以f(x)在[a,b]上有界。（严格来说这也是需要证明的，不过它的证明属于更深层次的数学分析内容，具体证明过程放在文末）

不妨设f(x)的最大值为M，最小值为m。则：

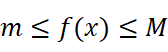
考虑两种情况：

当m=M时，f(x)≡m，此时

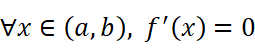
显然

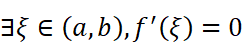
当m<M时，考虑到M和m两个数中至少有一个不等于f(a)，不妨令M≠f(a)

在(a,b)上，至少有一点ξ使f(x)取得最大值M

由于

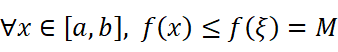
由费马引理知：

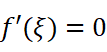
令m≠f(a)时证法同理。罗尔定理得证。

罗尔定理中要求

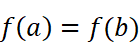
这一条件实在是太特殊了，很难出现应用场景。如何才能推广罗尔定理呢？让我们在下一节继续：《渐入佳境：拉格朗日中值定理》。

补充：连续即有界的证明。出处：高等教育出版社华东师大数学系编的数学分析。

我们先假设连续即有界。

所以连续即有界。