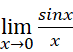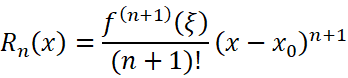“物理学的大厦已经基本建成了，后辈物理学家只要做一些零碎的修补工作就行了”，在世纪之交1900年时，威廉·汤姆森发表了这一次异常著名的演讲，“不过在物理学阳光灿烂的天空下，漂浮着两朵小乌云。”开尔文男爵的想法也代表了当时的物理学界。大家显然忽略了这两朵乌云的恐怖，谁也没想到，一场史诗级的风暴紧随其后。

以经典力学、经典电磁场理论和经典统计力学为三大支柱的经典物理大厦已经建成，难怪伟大的开尔文男爵也会感到陶醉，感到物理学已大功告成，断言往后难有作为了。而乌云似乎出现在无关紧要的地方：第一朵乌云出现在黑体辐射实验和理论的不一致（光的波动理论争议上），第二朵乌云出现在关于能量均分的麦克斯韦——玻尔兹曼理论上（发现光速不随运动参考系而变）。

不过，我们已经见证了物理学发展的历史：正是这两朵小小的乌云，让物理学再一次井喷式发展。

一：普朗克的惊天妙思：从黑体辐射说起

铁块的颜色一般不会是鲜艳的红色（如果谁手上的铁块是红色的，请立刻放下它并联系医生）。不过，对它充分加热后，会变成这个样子：

铁块会发出红黄色的光。我们知道，对于生活中能见到的任何物品，它都会吸收、反射，并辐射电磁波。吸收和反射我们姑且不谈，先来考虑一下电磁波的辐射：

任何一个物体都在向外辐射电磁波，这种辐射与物体的温度有关，称为热辐射。热辐射的强度与物体的温度、材料的种类和表面状况有关。于是我们假想出一种理想物体，叫做黑体。黑体辐射的强度只与温度有关，即：黑体是能够完全吸收投射到其表面的各种波长的电磁波而不发生反射的物体。

我们可以在在空腔壁上开一个很小的孔，射入小孔的电磁波在空腔内表面会发生多次反射和吸收，最终不能从空腔射出。这个带小孔的空腔就可以近似为一个绝对黑体：

根据实验结果，我们可以得温度与辐照强度和波长的关系：

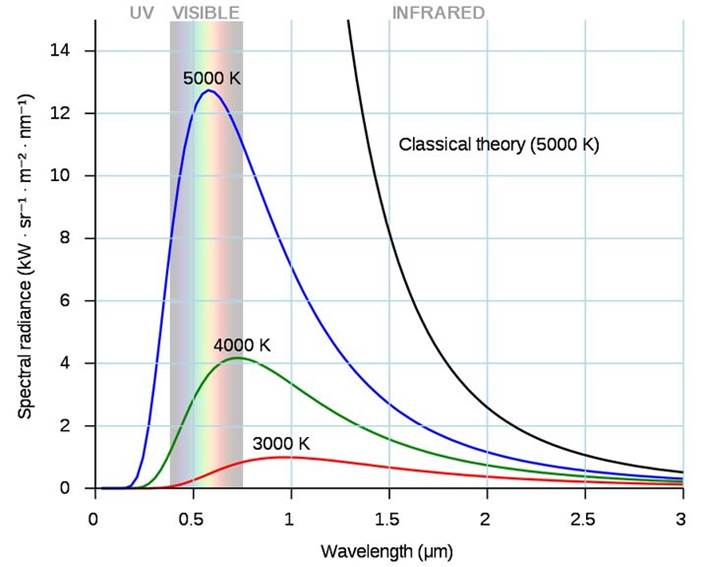
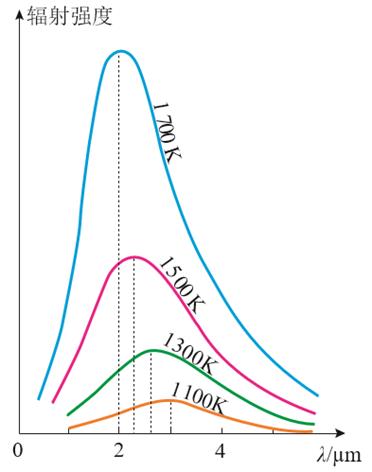
实验结论为：随着温度的升高，黑体辐射强度增强，且辐射强度的极大值向波长较短方向移动。于是，第一朵乌云出现了：没有任何一种理论可以比较完美地解释这个实验现象。黑体辐射实验结果和理论不一致。德国物理学家维恩在 1896 年、英国物理学家瑞利在1900 年，分别提出了辐射强度按波长分布的理论公式。他们提出的公式都只能解释一部分实验现象。维恩公式在短波区与实验非常接近，在长波区则与实验偏离较大；瑞利公式在长波区与实验基本一致，但在短波区与实验严重不符：

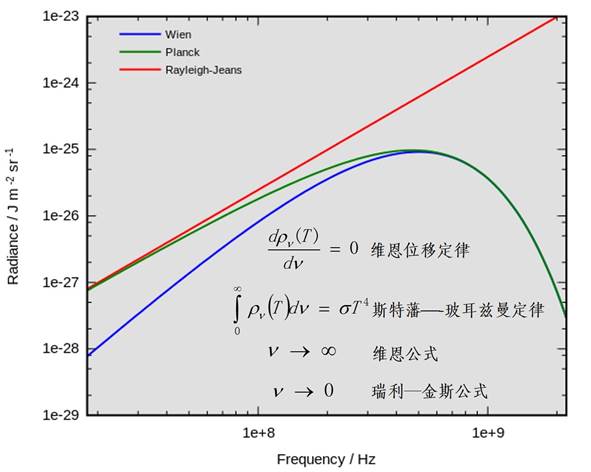
这时我们的普朗克站出来了。他提出来了一个震惊世人一百年的假定：组成黑体的振动着的微粒的能量只能是某一最小能量值 ε 的整数倍。例如，可能是 ε 或 2ε、3ε……他把这个不可再分的最小能量值 ε 叫做能量子。能量子的能量值由电磁波的频率决定：

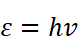
其中h就是大名鼎鼎的普朗克常量：

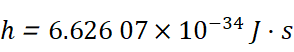
即：为微观粒子的能量是不连续的。换一种表述：微观粒子的能量是量子化的。

根据这种想法得到的公式真的完美拟合了黑体辐射实验结果：

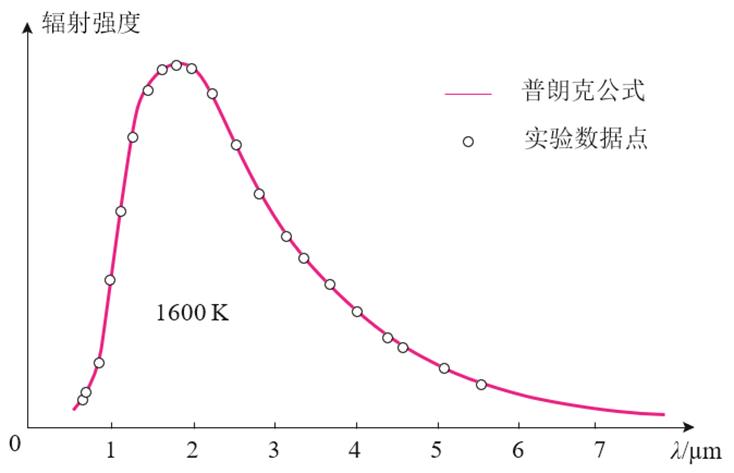
至此，量子力学的帷幕拉开了。普朗克正确地破除了“能量连续变化”的传统观念，这成为了新物理学思想的基石之一。

二：爱因斯坦横空出世：光电效应方程

我们需要先抛出一个问题：光究竟是什么？

在19世纪时，主流想法都认为光是一种波：从19世纪初开始，托马斯·杨、菲涅耳、马吕斯等分别观察到了光的干涉、衍射和偏振现象。19世纪60年代和80年代，麦克斯韦和赫兹先后从理论上和实验上确认了光的电磁波本质。这一切都印证这光的波动理论。

不过，在1887年，赫兹在研究电磁波的实验中非常偶然地发现，接收电路的间隙如果受到光照，就更容易产生电火花。这一现象引起许多物理学家的关注。勒纳德、汤姆孙等物理学家相继进行了实验研究，证实了这个现象：照射到金属表面的光，能使金属中的电子从表面逸出。这个现象称为光电效应。

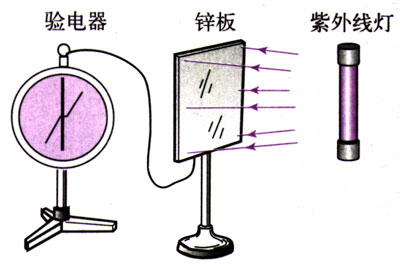
我们可以用一个电路来深入研究这个问题：

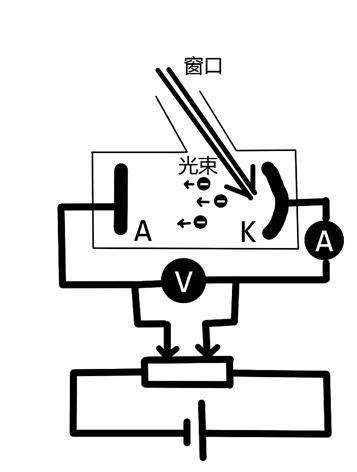
K和A是密封在真空玻璃管中的两个电极，K是光电材料，在受到光照时能够发射光电子。K与A之间电压的大小可以调整，电流的流向可以通过变阻器控制。

现在我们用不同颜色的光（即波长不同，即能量不同）照射K，K由于光电效应会溢出电子。接通电源后，在AK之间存在电场，两种不同的电场方向对应遏制或帮助电子达到接受电极A。    这时我们分别读取电流表（测出光电流大小）和电压表（测出施加电压的大小）的数据，可以作图如下：

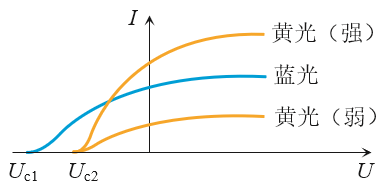
在一定的光照条件下，单位时间内K发射的光电子的数目是一定的。当施加反向电压达到一定值时，所有电子都无法到达A，这时的电压我们称为截止电压。当施加的正向电压达到一定值时，所有光电子都被A吸收，这时即使再增大电压，电流也不会增大，这时的电流我们称为饱和电流。

当我们改变入射光的波长时，发现：当入射光的频率减小到某一数值时，光电流消失，无论光照强度有多大都完全不产生光电子。我们把这个频率叫做这种光电材料的截止频率或极限频率。实验表明，不同金属的截止频率不同。即截止频率由金属自身的性质决定。

对于同一种金属，对于一定频率的光，无论光的强弱如何，截止电压都是一样的。光的频率改变时，截止电压也会改变。这意味着，对于同一种金属，光电子的能量只与入射光的频率有关，而与入射光的强弱无关。

另外一个值得注意的实验结果是：当频率超过截止频率时，无论入射光怎样微弱，照到金属时会立即产生光电流。精确测量表明产生电流的时间很快，光电效应几乎是瞬时发生的。

我们再回顾一下光电效应是什么：照射到金属表面的光，能使金属中的电子从表面逸出。我们知道，金属中原子外层的电子会脱离原子而做无规则的热运动。但在温度不很高时，电子并不能大量逸出金属表面，这是因为金属表面层内存在一种力，阻碍电子的逃逸。电子要从金属中挣脱出来，必须获得一些能量，以克服这种阻碍。 要使电子脱离某种金属，需要外界对它做功，做功的最小值叫作这种金属的逸出功。根据进一步实验表明，不同金属的逸出功一般不同。即逸出功由金属自身的性质决定。

当时物理学界主流观点认为光是一种波。但这种理论无法解释这几个现象：金属为什么存在极限频率？（如果光仅仅是波，那么对于任一频率的光，照射在金属板上，只要光强足够大，也就是波幅足够大，传给电子的能量一定会大到使电子逸出。）逸出电子的最大动能为什么与光强无关？（如果光仅仅是波，那么随着光强的增大，也就是波的振辐越大，则电子振动越剧烈，逸出电子的动能理应越大。然而逸出电子的最大动能与光强无关。）为什么从开启入射光束到检测到电流的时间间隔极短？ （如果光仅仅是波，那么电子必须累积来自入射光束的能量，直到获得足够能量才能逃逸离开金属表面。但电子几乎是瞬时发射的。）

带着这三个问题，我们的爱因斯坦横空出世了。为了解释光电效应，爱因斯坦在1905年发表了题为《关于光的产生和转化的一个试探性观点》的文章。他假定电磁波本身的能量也是不连续的，光由一个个不可分割的能量子组成的。即：光束是由一群离散的能量粒子组成，称为光量子。频率为v的光的能量子为hv，其中，h为普朗克常量。这些能量子后来称为光子。

按照爱因斯坦的理论，当光子照到金属上时，它的能量可以被金属中的某个电子全部吸收，金属中的电子吸收一个光子获得的能量是hv，在这些能量中，一部分大小为W0 的能量被电子用来脱离金属（即逸出功），剩下的是逸出后电子的初动能，即:

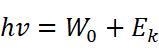
我们应该如何验证这个公式呢？光电子的动能非常难以测定。但是，截止电压Uc是容易测得的。当电压为截止电压时，以最大初速度向吸收电极射出的光电子刚好不能达到电极。我们可以据此得出：

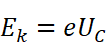
所以：

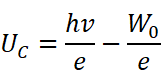
密立根正是通过这个公式，开始以他标志性的精湛技术测量光电效应中的两个物理量：测量金属的截止电压Uc与入射光的频率v，由此算出普朗克常量h，并与普朗克根据黑体辐射得出的h相比较，以检验爱因斯坦光电效应方程的正确性：

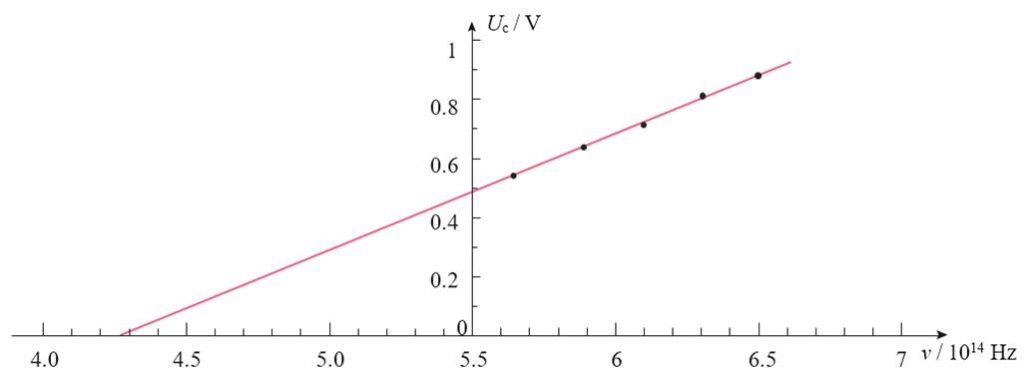
实验的结果是，两种方法得出的普朗克常量h在0.5%的误差范围内是一致的。这为爱因斯坦的光电效应理论提供了直接的实验证据。光电效应的实验一定程度上说明了光是具有粒子性的。

三：狭义相对论：最优美而著名的物理方程

大概绝大多数人都听说过这几个字吧：狭义相对论。它有名到，只要聊到物理甚至哲学就想提它两句。不过，说世界上只有几个人能看懂相对论肯定是扯淡。

什么是“相对”呢？设想：一条河流中的水以相对于河岸的速度v水岸流动，河中的船以相对于河水的速度v船水顺流而下。在经典力学中，船相对于岸的速度v船岸＝v船水＋v水岸。经验告诉我们，这简直就是天经地义的。

但是大家可以从这个角度重新考虑这个问题：这个关系式涉及两个不同的惯性参考系，而速度总是与位移（即空间长度）及时间间隔的测量相联系。在牛顿看来，位移的测量、时间的测量都与参考系无关。在这种时空观念下，上式才成立。

不过，使用经典力学考虑船和水这个问题是绝对没有问题的。但是，像一切科学一样，经典力学没有也不会穷尽一切真理，它也有自己的局限性。 从地面上物体的运动到天体的运动，从大气的流动到地壳的变动，从拦河筑坝、修建桥梁到设计各种机械，从自行车到汽车、火车、飞机等现代交通工具的运动，从投出篮球到发射导弹、人造卫星、宇宙飞船……所有这些都服从经典力学的规律。但是，上面提到的各种物体的运动，速度都远远小于真空中的光速。

把我们的视角放在光速的尺度上：假设人类研究出了速度为光速一半的飞船，飞船头部射出激光，我们站在飞船前方观察这束激光，那激光的速度是多少呢？答案似乎应该是一点五倍的光速。按照惯例，是时候有人站出来说：不是这样的！

1887年，迈克尔逊和莫雷在美国克利夫兰做了一个仪器（称为迈克尔逊干涉仪），来测量两垂直光的光速差值。

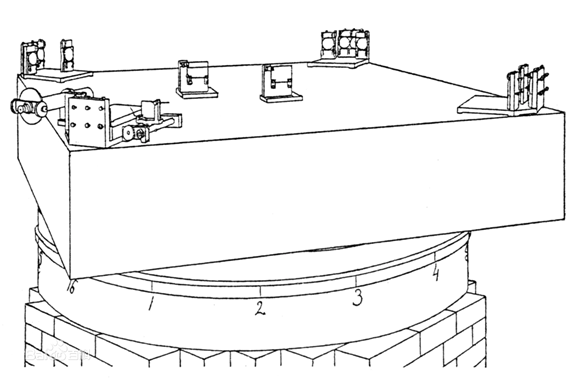
实验内容读者可以自行了解。迈克尔逊－莫雷实验证明了光速在不同惯性系和不同方向上都是相同的（同时否认了以太（绝对静止参考系）的存在，以太的争论也是一段很有趣味的科学史）。

1905年，爱因斯坦认为既然光速不变，于是抛弃静止参考系，以光速不变原理和狭义相对性原理为基本假设的基础上建立了狭义相对论。这是一种崭新的时空观念。他指出，在研究物体的高速运动（速度接近真空中的光速）时，物体的长度即物体占有的空间以及物理过程、化学过程，甚至还有生命过程的持续时间，都与它们的运动状态有关。这样，空间和时间不再与物体及其运动无关而独立存在了。

作为狭义相对论两个基本原理的直接推论，就是同时的相对性，即在一个参考系中同时发生的事件，在另一个参考系中不再同时。假设一列高铁沿直线轨道以匀速 v 向右运动，车厢中央的光源在时刻 t = 0 发出一个闪光，如果车厢长度为 2L，则经过时间 L/C后闪光分别到达车厢的前壁和后壁。对于车厢里的观察者来说，车厢是惯性系，光向前及向后的传播速度相同，传播的距离相同，因此闪光同时到达车厢的前壁及后壁，即这两个事件对车上的观察者来说是同时发生的  但地面上的观察者不这么认为，因为当闪光向车厢前壁传播时，车厢也在以速度 v 向前运动，因此，闪光到达前壁的距离要此到达后壁的距离长一些，而光速是不变的，所以在地面的观察者看来，闪光先到达车厢后壁，后到达车厢前壁。即对地面上的观察者而言，这两个事件不是同时发生的。

现在我们来量化这一过程。假设一列高铁沿直线轨道以匀速 v 向右运动，车厢地板上一个光源向上发出一个闪光，被车厢顶部的反射镜反射回车厢地板，并用一个钟记录下光脉冲来回运动经历的时间。

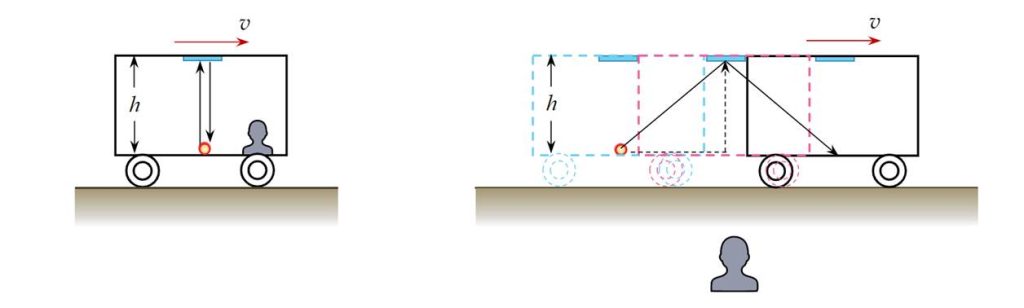
假设车厢高度为 h，因为光速为 c，所以车厢里的观察者看到的时间间隔为

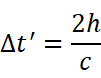
但在地面上的观察者看来，当光脉冲向上传播和返回时，车厢同时在以匀速 v 向右运动，因此光脉冲的路径是等腰三角形的两条斜边，如果光脉冲来回的时间间隔是 Δt，则有：

我们联立两个时间间隔，通过简单的解方程，可以得到：

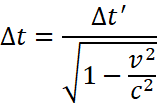
这个系数很常用，我们令：

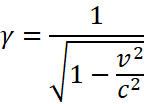
显然：

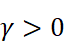
所以：

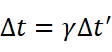
即在惯性系中，运动的钟（即高铁上的钟）比静止的钟要走得慢。这个结论称为狭义相对论的时间膨胀或钟慢效应，这体现了时间的相对性。我们把在自身静止的参考系内测得的时间称为固有时。显然，固有时的时间间隔是最短的。

必须说明，时间膨胀或钟慢效应并不是钟的问题，而是由狭义相对论的时空性质导致的。一个静止的观察者会发现匀速运动参考系中所有的物理过程都变缓了，甚至生命进程也变缓了。而在这个运动参考系中的观察者却认为一切正常，并不觉得自己看到的一切在变缓。由于运动是相对的，两个互相做相对运动的参考系中的观察者会认为对方的钟都在变慢。

对了，为什么在生活中体会不到这种效应？不妨随手计算一下：对于速度 v1 = 300 km/h的高铁、速度 v2 = 7.9 km/s的地球同步卫星和开头提到的速度 v3 = 0.5 c 的飞船，各自的时间膨胀效应有多大：

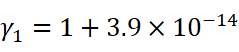
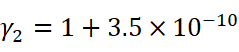
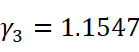
前两个的数量级明显是可以忽略的。

物体长度的测量和同时性密切相关，如果要测量一个直杆的长度，在相对直杆静止的参考系内，只需测出直杆两端的位置然后求出位置的差即可。因为直杆是静止的，所以两端位置的测量并不要求是同时的。但如果直杆是运动的，要测出直杆的长度，就必须同时测出两端的位置，否则测出的就不是直杆的长度了。既然同时性是相对的，那么长度的测量也一定是相对的。根据同时的相对性可以得出：

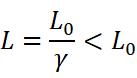
其中 L 为地面观察者测得的直杆长度，L0 为在相对直杆静止的坐标系内测得的长度，称为固有长度。因此，狭义相对论告诉我们，物体沿运动方向的长度会缩短，这个结果称为尺缩效应，这就是长度的相对性。

应当指出，长度收缩也是相对的，一列高铁过桥时，桥上的观察者认为高铁变短了，而高铁上的观察者认为是桥变短了。另外，长度收缩只发生在平行于运动的方向上，垂直于运动方向的长度没有收缩。

同理，牛顿力学经过修改后可以改写成相对论性力学，即符合狭义相对论的形式，但质量的定义要修改为：

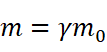
m 称为物体的运动质量，而 m0 则称为物体的静止质量，即物体在自身静止的参考系中的质量。由上式可见，物体的运动速度越大，相应的运动质量也就越大，并且任何静止质量不为零的物体其运动速度都不可能等于或大于光速，否则运动质量将变成虚数或无限大，这是没有意义的。同时也可以看到，通过外力作用将物体加速到光速也是不可能实现的。

进一步可以推出狭义相对论的另一个重要结论，就是爱因斯坦质能关系(这个式子简直太有名了)：

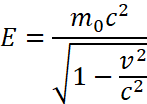
于是郑重地得到：

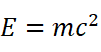
即一定质量的物质就具有与之相当的一定的能量。由质能关系可知，即使是 1 g 的物质也蕴藏着巨大的能量。爱因斯坦的质能关系是核能开发利用的理论基础，人类从此就进入了核能利用的新时代。

四：康普顿效应：光子除了能量之外还具有动量

白天的时候抬头看天空，天空各处都是亮的；但航天员在大气层外飞行时，尽管太阳的光线耀眼刺目，其他方向的天空却是黑的，甚至可以看见星星。这是为什么？

天空本来是没有颜色的，只是由于大气分子的存在，当太阳光入射到地球上的时候被散射了。光在介质中与物质微粒相互作用，因而传播方向发生改变，这种现象叫做光的散射。如果大家知道：波长越短，散射强度越强，就知道蓝紫光被散射得最厉害，因此天空呈现蔚蓝色。不呈紫色的原因是：紫光被大气吸收了，且人眼对紫光不敏感。如果设想地球没有大气层，那看到的天空应该时时刻刻是现在的夜晚，除了恒星以外一片漆黑。同理，海水的蓝色也是因为水分子的散射造成的，如果你走近了看，海水是透明无色的。另外，离得越远越深的海水，蓝色也越深甚至发黑，那是因为远/深处海水的散射光被你接收到的光变少了，所以呈现出深黑色。

1918-1922年，美国物理学家康普顿在研究石墨对X射线的散射时，发现在散射的X射线中，除了与入射波长λ0相同的成分外，还有波长大于λ0的成分，这个现象称为康普顿效应。糟了，这又是传统物理学无法解释的。按照经典物理学的理论，由于光是电磁振动的传播，入射光引起物质内部带电微粒的受迫振动，振动着的带电微粒从入射光吸收能量，并向四周辐射。这就是散射光。散射光的频率应该等于带电粒子受迫振动的频率，也就是入射光的频率，因而散射光的波长与入射光的波长应该相同，不会出现λ＞λ0的散射光。经典理论与实验事实又一次出现了矛盾。

康普顿用光子的模型成功地解释了这种效应。他的基本思想是，X射线的光子不仅具有能量，也像其他粒子那样具有动量，X射线的光子与晶体中的电子碰撞时要遵守能量守恒定律和动量守恒定律，求解这些方程，可以得出散射光波长的变化值Δλ。理论结果与实验符合得很好。

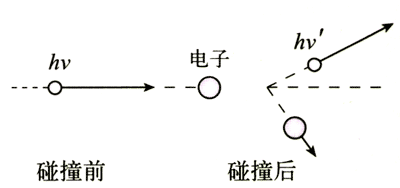
光电效应和康普顿效应深入地揭示了光的粒子性的一面。前者表明光子具有能量，后者表明光子除了能量之外还具有动量：

在狭义相对论中我们已经知道：

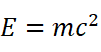
一个光子的能量是：

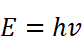
联立得：

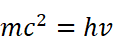
得到光子的质量为（必须说明，这里得出的光子质量是它的相对论质量。由于光子不能静止下来，所以它没有静止质量。）：

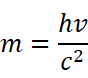
由于光是一种波，所以：

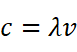
可以求得光子的动量为：

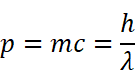
在康普顿效应中，当入射的光子与晶体中的电子碰撞时，要把一部分动量转移给电子，因而光子动量变小。动量p减小意味着波长λ变大，因此有些光子散射后波长变大。从动量守恒定律和能量守恒定律出发，按照动量和能量表达式对康普顿效应做定量分析，其结论与实验事实符合得很好。

五：德布罗意的大胆构思：粒子的波动性

回到一个重要的问题：光的本质是什么？从前文的一切，我们已经充分地认识到了光既是粒子，又是波，即光具有波粒二象性。这种性质会是只有光才有的吗？

1924年，法国巴黎大学的德布罗意考虑到普朗克能量子和爱因斯坦光子理论的成功，在博士学位论文中大胆地把光的波粒二象性推广到实物粒子，如电子、质子等。他写道：“整个世纪以来，在光学上，与波动方面的研究相比，忽视了粒子方面的研究；而在实物粒子的研究上，是否发生了相反的错误呢？是不是我们把粒子方面的图像想得太多，而忽视了波的现象？”于是，他提出假设：实物粒子也具有波动性，即每一个运动的粒子都与一个对应的波相联系，而且粒子的能量ε和动量p跟它所对应的波的频率ν和波长λ之间，也像光子跟光波一样，遵从如下关系：

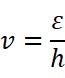
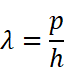
这种与实物粒子相联系的波后来称为德布罗意波，也叫做物质波。这是很难想象的，大家不妨设想一下高铁的波动性。连爱因斯坦都吐槽：“Look at it, it seems crazy, but it does hold up!”虽然爱因斯坦肯定了德布罗意关于物质波的想法，但真正判定德布罗意的假说是否“hold up”的还只能是实验。我们知道，光的干涉和衍射现象是光具有波动性的有力证据。因此，如果电子、质子等实物粒子也真的具有波动性，那么它们就应该像光波那样，也能发生干涉和衍射。光虽然具有波动性，但并不是任何情况下都能发生明显的干涉和衍射。用来显示波动性的狭缝或障碍物的线度要足够小才行。人们该如何制作或找到这样的装置？在20世纪20年代，那些想要用实验验证物质波的物理学家们（说起来实在幸运，因为在技术上的这一难题已经解决）在对伦琴射线的研究时解决了。

1912年，德国物理学家劳厄提议，利用晶体中排列规则的物质微粒作为衍射光栅，来检验伦琴射线的波动性。实验获得了成功，证实伦琴射线就是波长为十分之几纳米的电磁波。考虑到电子的德布罗意波长与伦琴射线的波长具有相近的数量级，1927年戴维孙和GP汤姆孙（大家可能对他爸JJ汤姆孙发现电子有印象）分别利用晶体做了电子束衍射的实验，得到了这样的衍射图样，从而证实了电子的波动性：

除了电子以外，后来还陆续证实了质子、中子以及原子、分子的波动性。对于这些粒子，德布罗意给出的两个关系同样正确。

宏观物体的质量比微观粒子大得多，它们运动时的动量很大，对应的德布罗意波的波长就很小。例如，一个质量为0.01 kg，速度为300 m/s的子弹，它的德布罗意波长只有2.2×10-34 m，比宏观物体的尺度小得多，根本无法观察到它的波动性。而一个原来静止的电子，在经过100 V电压加速后，德布罗意波长约为0.12 nm，因此有可能观察到电子的波动性。

对了，1929年，德布罗意获得了诺贝尔物理学奖，成为前无古人后无来者以学位论文获此殊荣的人。祝大家的学位论文也能拿个诺奖玩玩。

六：双缝干涉实验和概率波：粒子性和波动性能集于一身

在经典物理学的观念中，粒子有一定的空间大小，有一定的质量，有的还具有电荷。它们的运动遵从牛顿第二定律，所以只要已知它们的初始位置和初始速度，就可以准确地确定以后任意时刻的位置和速度，进而在空间描绘出确定的轨迹。因此，任意时刻的确定的位置和速度以及时空中的确定的轨道，是经典物理学中粒子运动的基本特征。与粒子不同，经典的波在空间是弥散开来的，其特征是具有频率和波长，也就是具有时空的周期性。

显而易见：在经典物理学中，波和粒子是两种不同的研究对象，具有非常不同的表现，就像牛唇和马嘴的关系一样。 

我们先来考虑我们的老朋友：光子。学习过机械波的读者一定知道这个经典的实验：双缝干涉。

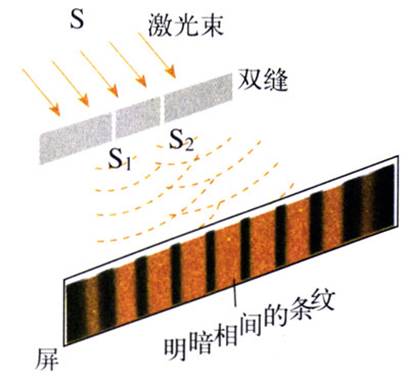
从光源S发出的光通过双缝S1和S2后在屏上形成明暗条纹。按照光的波动理论，条纹的明暗表示到达屏上的光的强度不同。按照光子的模型，每个同频光子都带有相同的一份能量，所以条纹明暗的分布表示到达屏上的光子数目多少的分布。因此，光的强弱对应于光子的数目，即明纹处到达的光子数多，暗纹处到达的光子数少。

干涉现象是波动性的有力证明。但，我们是否可以认为，在一束光中，是光子之间的相互作用使它表现出了波动性，而不是光子本身就具有波动性呢？

为此，我们可以使光源S非常弱，以至它在前一个光子到达屏幕之后，才发射第二个光子，这样就排除了光子之间相互作用的可能性。实验结果表明，尽管单个光子的落点不可预知，但是长时间曝光之后，仍然得到图中所示的条纹分布。

可见，光的波动性不是光子之间的相互作用引起的，而是光子自身固有的性质。

现在的问题是，单个光子通过狭缝后到底落在屏上的哪一点呢？

1926年德国物理学家玻恩认为：虽然不能肯定某个光子落在哪一点，但由屏上各处明暗不同这个事实可以推知：光子落在各点的概率是不一样的。光子落在明纹处的概率大，落在暗纹处的概率小。这就是说，光子在空间出现的概率可以通过波动的规律确定。所以，我们称光波是一种概率波。

对于电子和其他微观粒子，由于同样具有波粒二象性，所以与它们相联系的物质波也是概率波。也就是说，单个粒子的位置是不确定的，但在某点附近出现的概率的大小可以由波动的规律确定。对于大量粒子，这种概率分布导致确定的宏观结果，例如衍射条纹的分布等。

这张图是电子通过双缝的结果。图甲表示100多个电子通过双缝后的干涉图样，可以看到，每一个电子都是一个点，这体现了电子的粒子性。图乙、丙分别表示3 000多个、70 000多个电子通过双缝后的干涉图样。随着电子数的增加，规则的条纹越来越明显。

七：单缝衍射实验：不确定性关系

我们来考虑光的单缝衍射实验。由于衍射，光子到达屏上的位置会超出单缝投影的范围。（其他粒子也具有波动性，所以其他粒子经过单缝时也有同样的现象）分析实验，我们发现我们无法同时用质点的位置和动量来描述微观粒子的运动。单缝衍射时，屏上各点的亮度反映了粒子到达这点的概率。如果把这个概率的分布在坐标系中表示出来，就是右侧的曲线。

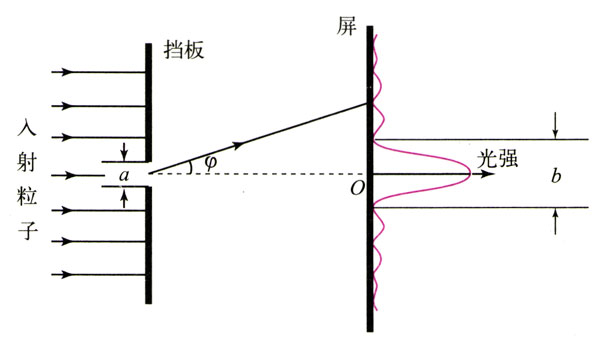
入射的粒子有确定的动量，但它们可以处于挡板左侧的任何位置，也就是说，粒子在挡板左侧的位置是完全不确定的。对于通过挡板狭缝的粒子则可以说，它们的位置被狭缝限定了，它们的位置不确定量减小了（不过我们仍然不能准确地说出射到屏上的粒子在通过狭缝时的准确位置，因为缝有一定的宽度a）。从下面的分析可以知道，粒子的动量的不确定量增大了：微观粒子具有波动性，会发生衍射，大部分粒子散布在宽度为b的中央亮条之内。这些粒子在到达狭缝之前沿水平方向运动，而在经过狭缝之后有些粒子跑到缝的投影位置以外，我们可以说这些粒子具有了与其原来运动方向垂直的动量。由于粒子到达屏上的位置完全是随机的，所以粒子在垂直方向上的动量具有不确定性。不确定量的大小可以由中央亮条的宽度来衡量。

为了更准确地测定通过狭缝的粒子的位置，我们可以选用更窄的狭缝。但是，从衍射的规律可以知道，狭缝越窄，屏上中央亮条就越宽。这表明，尽管更窄的狭缝可以更准确地测得粒子的位置，但粒子动量的不确定量却更大了。

利用数学方法对微观粒子的运动进行分析（推荐阅读：https://zhuanlan.zhihu.com/p/136381273）可以知道，如果以Δx表示粒子位置的不确定量，以Δp表示粒子在x方向上的动量的不确定量，那么：

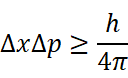
式中h是普朗克常量。这就是著名的不确定性关系。

在微观物理学中，不确定关系告诉我们，如果要更准确地确定粒子的位置（即Δx更小），那么动量的测量一定会更不准确（即Δp更大），也就是说，不可能同时准确地知道粒子的位置和动量，因而也就不可能用“轨迹”来描述粒子的运动。我们不可能准确地知道单个粒子的运动情况，但是我们可以准确地知道大量粒子运动时性的统计规律。一个宏观系统总是包含着大量粒子，因此我们仍然能够对宏观现象进行预言。例如，当粒子数很少时，我们不能预言粒子通过挡板上的狭缝后落在屏上的位置，但却可以准确地知道粒子落在屏上某点的概率；概率大的位置正好是某种波通过狭缝发生衍射时产生亮条的位置。

八：在这里停下吧：后记

不知不觉写了一万多字。作为波粒二象性的简单介绍已经足够了。我不想在这篇小文中运用过多的数学和物理知识，所以继续深入也不太可能了。不过，文章中提到的内容应该可以大致描绘出近代物理的一部分画卷。

我不太清楚这篇文章的受众应该是什么。因为它需要一定的数学物理知识（应该高中水平足够），但并没有什么深度。但也一定不适合将要深入学习物理的大佬们。所以文章可以归属到我自娱自乐的那部分。相应地，文章中为了简便而不严谨的地方会比较多，但应该没有原则性的错误（若有请务必指出）。

但这篇文章其实只揭开了面纱的一角，甚至还没有到精彩的地方（比如在化学中的应用，包括波函数等等一些有趣的东西），一些非常值得深入讨论的地方也一笔带过（比如能再聊一万字的双缝干涉实验）。我有机会一定会继续写下去，就当作对自己掌握程度的检验吧。

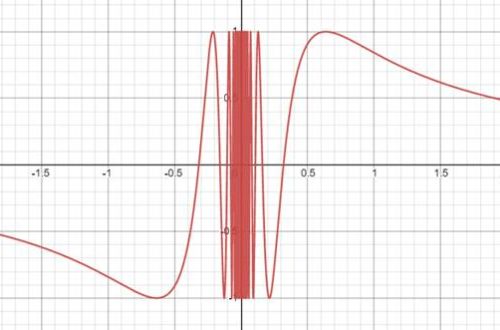
最后一定要献上这张图：