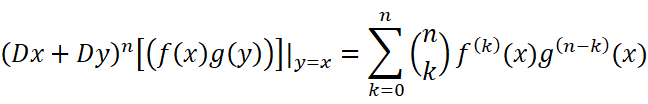
【高数学习回顾】4.莱布尼茨公式，但是二项式定理

这篇小短文里我不打算用数学归纳法再证明一遍莱布尼茨公式和二项式定理。这种证明方法已经遍布教材和网络，非常完善且有点….无聊？但是非常有意思的一点是，这二者形式上是非常类似的：

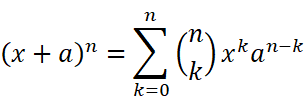
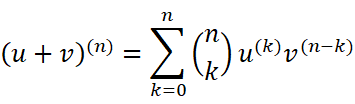
在用数学归纳法证明这两个公式时，可以直观地感受到证法的套路是一模一样的。但是这种直观的感受应该如何描述出来呢？

我们很容易想到，(u+v)的n次方一定可以像这样展开：

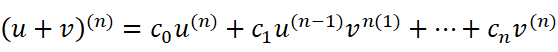
这意味着无论我们想求得这个展开式的哪一项，都要选择n次v或者u，直到二者的幂之和为n。我们再类比一下在二项式中的情况：

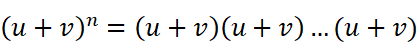
也是需要选择n次v或者u，直到二者的幂之和为n，这才成为最后二项式定理中的一项：

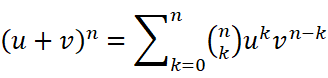
自然而然，我们假想的系数正是考虑二者组合方式的个数。所以可以类比得到我们的莱布尼茨公式：

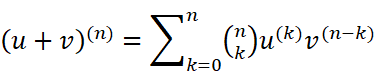
要是仅仅如此也太不像我的风格了。（毕竟还没写几个字呢）

故事还要从我在某天上课摸鱼说起。我在迷迷糊糊中，突然发现了两个奇妙的式子：

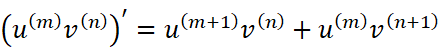
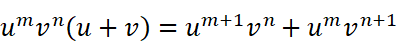
这个巧妙的相似直接让我再也听不进去老师说的一个字（太对不起老师了），如果这样思考：求一次导可以类比为乘以(u+v)，求n次导能不能类比为乘以(u+v)的n次方呢？这样就可以把高阶导数和二项式定理联系起来了。

顺着这个思路我查阅了一些资料。发现求导是可以用线性算子表示的（求导是个线性运算大家应该都知道吧）。随之发现了一种技巧性非常强的证明莱布尼茨公式的方式。这是出自楼红卫《数学分析注记》里的一种方法，看完让我直呼过瘾。现在我把这种方法用较为简单的方式描述出来：

我们用Dx表示对x求导，Dy表示对y求导，我们可以得到这样一个式子（也是整个步骤中最有技巧性的一步）：

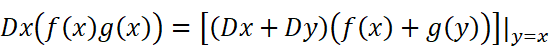
这个式子显然成立。不妨再把它写成：

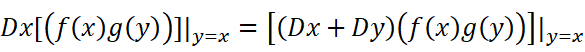
以这个为前提，我们可以开始考虑n阶导数：

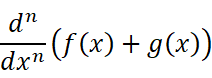
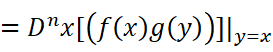
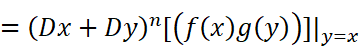
这不就直接出现了二项式定理了嘛！！很轻松就可以得到

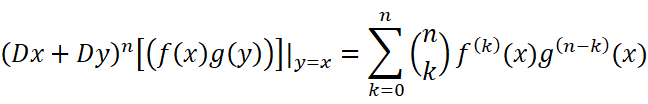
这个证明方式优美得就像….呃，人体曲线？毕竟二者都具有对称的美感（虽然我也觉得这个比喻很离谱）。但其实也并非完全一致，曲线是直接呈现出来的对称，而二项式定理和莱布尼茨公式间是潜藏但是能直观感受到的一种对称。