前文回顾：我们已经通过费马引理证明了罗尔定理：

 若

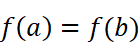
则

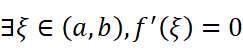
要如何推广这一定理呢？

渐入佳境：拉格朗日中值定理

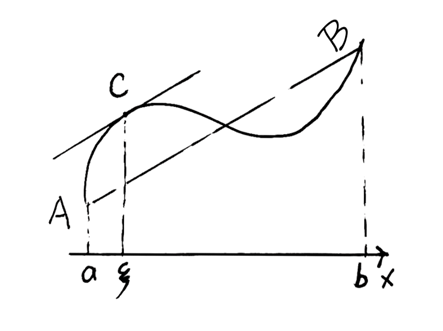
我们观察一个不符合罗尔定理条件的函数：

然后稍稍把它旋转一下…

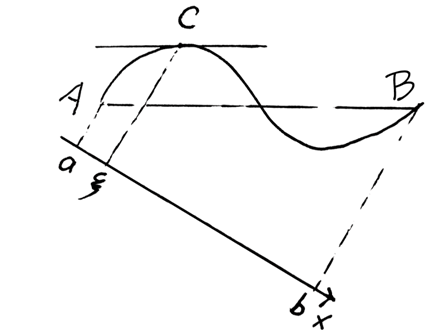
这不就回到罗尔定理了嘛！把AB方向看作x轴，根据罗尔定理可以得到：

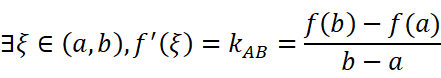
等等！这个证明非常非常不严密（ ξ明明在真正的x轴上），但是我们猜都能猜到这个式子肯定是成立的。那就以证明这个式子为目标吧：

有请拉格朗日中值定理出场：

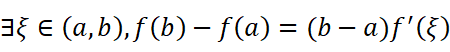
有了前文的思路，我们不妨通过构造罗尔定理来证明朗格朗日中值定理。我们假设：

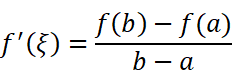
不妨令：

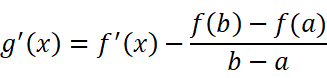
构造出：

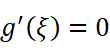
对它积分求得原函数：

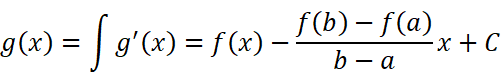
我们有没有可能构造出这样一个g(x)，使g(a)=g(b)呢？这样就可以应用罗尔定理了。

聪慧的我们不难发现，这显然是可能的。有两种方法可以构造出来：

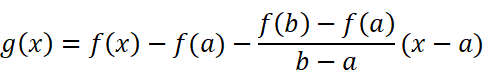
或者：

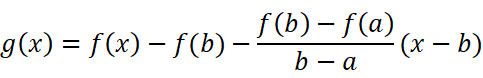
这样我们就有了证明拉格朗日中值定理的完整思路了。我们就取第一种构造方法，对朗格朗日中值定理进行证明吧：

证明：

令：

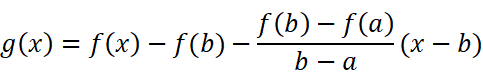
其中

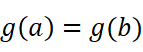
则有：

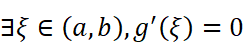
其中

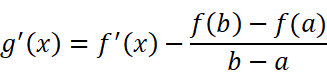
则

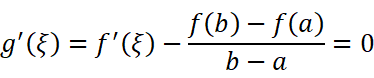
知：

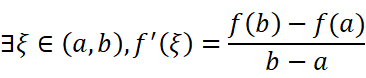
移项得：

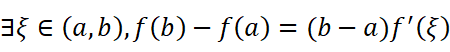
证毕。

我们再次观察拉格朗日中值定理与罗尔定理。不难发现，当f(a)=f(b)时，拉格朗日中值定理自然又会退化为罗尔定理。

拉格朗日中值定理的重要性我就不赘述了。我们现在想想我们还能通过它推导出来些什么，敬请见证下一节：《曲径通幽：柯西中值定理》