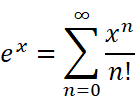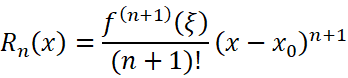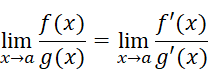学术-Into the Cosmos
-
【生物化学】2.蛋白质的结构层级:讨论生物信息的时候我们在说些什么?
本文利用AlphaFold模拟了数十种蛋白质的三维结构,讨论了蛋白质的结构层级,以及近代生物信息话题中的主要内容。
-
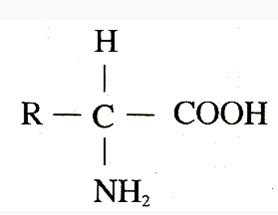
【生物化学】1.氨基酸的发现和结构及分类
蛋白质是生命功能里最重要的物质之一。组成蛋白质的基本单位是氨基酸。要学习生物化学,就从氨基酸开始吧。
-
【建站笔记】修复使用SSL证书时无法加载图片的错误
在网站迁移前,图片的URL格式是以IP命名的,如: 43.138.xxx.xxx/uploads/2023/06/image006-15.png 转移到域名后,原本图片的链接发生了从http到https无法识别的问题。 …
-
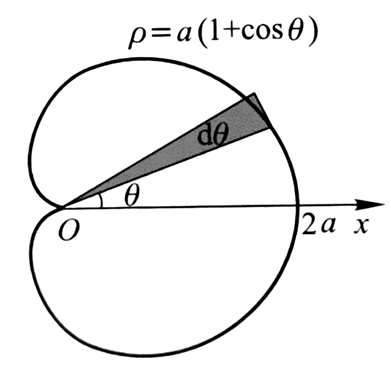
【高数学习回顾】13.定积分的几何应用:弧长、面积和体积
我们需要找到的是面积增量与x或y的增量的关系。通过升维、降维,定积分可以在几何应用中求出弧长、面积和体积
-
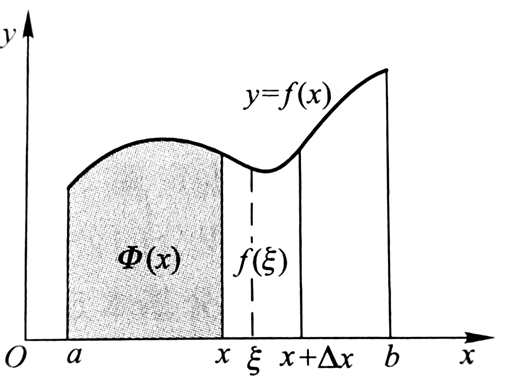
【高数学习回顾】12.走进定积分:积分上限的函数和牛顿-莱布尼茨公式
在学运动学时,大家肯定都遇到过这样的一个问题:如果一个车做变速运动,怎么求它所经过的路程?我们把问题抽象一下,可以变成:已知函数f(x),求它在某个区间与x轴围成的面积。我们应该如何解决这个问题呢?根据极限的思维,我们可…
-
【高数学习回顾】11.导数应用的实例:曲率到底是什么?
我们假设这个圆是由一条线弯曲绕成的,那在两个圆中,哪一条线弯曲程度更大呢?个圆半径越小,看起来就越弯曲;半径越大,看起来就越平。如果让半径趋于无穷大,圆看起来就像一条直线,就几乎不弯曲了。我们希望定义一个量来衡量几何体的…
-
【高数学习回顾】10.常用的麦克劳林公式:怎么记这些鬼东西?
麦克劳林公式在拟合函数方面很常用。看看一些常用的麦克劳林公式,他们长得好吓人,打死我也不愿意去硬背它们。那有没有什么方法能迅速地记住它们呢?
-
【高数学习回顾】9.筑基导数应用的大厦:泰勒公式和麦克劳林公式
对于一些较为复杂的函数(如:y=exp(x) ),为了便于研究,我们可能希望用一些简单的函数来近似表达。最常用的一种近似表达就是多项式。多项式具有一个非常优良的运算性质:只要对自变量进行有限次加减乘三种算数运算,就能求出…
-
【高数学习回顾】8.筑基导数应用的大厦:洛必达定理
洛必达是一个爱好数学的贵族,重金求伯努利给他补习数学。当时正是微积分的初创期,于是洛必达提出要购买伯努利的研究成果,并整理成了一本书:《无穷小量分析》。他在前言中提到了绝大多数成果来自伯努利和莱布尼茨,而洛必达法则正是书…
-
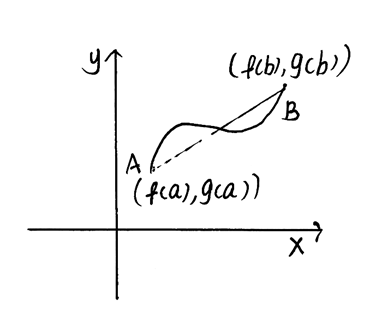
【高数学习回顾】7.筑基导数应用的大厦:柯西中值定理
如果不小心在使用拉格朗日中值定理时,同时写出了两个式子,你可能会发现它们有个共同的因数(b-a)。如果把两者相除消去公因式会得到什么呢?柯西中值定理是拉格朗日中值定理在参数方程形式下的表达形式