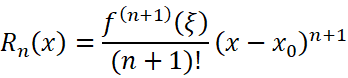【随处可见的物理】2.交流电的有效值是什么？

交流电的大小和方向是变化的，这导致电路中的测量和计算有诸多不便。有没有一种办法，可以便捷地表示交流电的特性呢？

于是我找来一个奇妙的电水壶，假装在里面灌满水，用家里的电源开始加热它。一段时间后水开了，记录下烧开一壶水所需时间。假如我能找到一个直流电源，用同样的时间把一壶水烧开了，那这段时间两种电源的平均热功率是不是等价的呢？

这个模型不严谨的地方太多了，我已经懒得一个一个找出来。但是这提供了一个定义交流电有效值的思路：在一个周期内，交流电和直流电通过电阻时产生的热量相等，就把直流电流（电压）的大小作为交流电流（电压）的有效值。

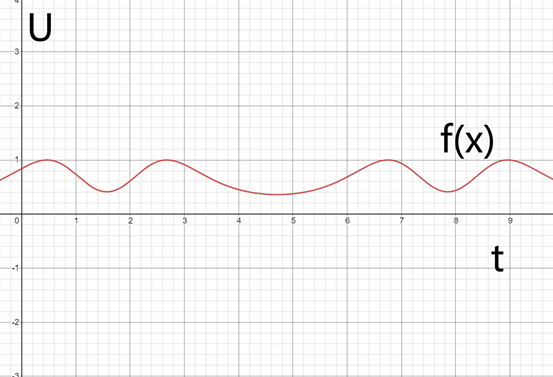
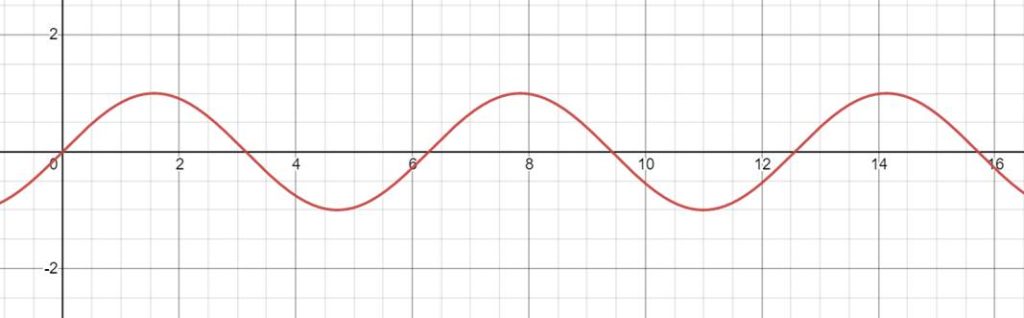
为了可视化，我随便写了一个函数（f(x)=sin(exp(sin(x))) ，不过这个函数是什么不重要），现在我们来尝试表示任意最小正周期为T的函数f(t)的有效值。

我们开始建立等式。考虑到

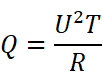
运用定积分的思想，把一个周期T内分为n个小区间，在每个小区间内任取一点ξ_i，令λ为所有区间长度的最大值，可以得到这样的等式：

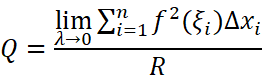
运用定积分的知识，很容易可以化为这种便于求解的形式：

这样就可以建立求得电压有效值U_RMS的通式：

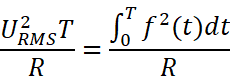
即：

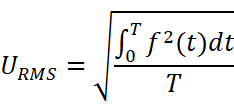
同理，假设f(x)是t关于I的函数，可以把电流有效值I_RMS表示为：

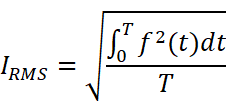
整个过程非常容易（枉费了我高中两年的困惑）。只要给出电流（电压）随时间变化的函数，我们就能给出电流（电压）的有效值。

下面不妨通过一个最经典的例子作为公式的应用场景。

对于正弦交流电f(t)=sinx：

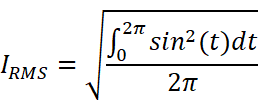
这个积分的求解是容易的。只需要先对它降幂：

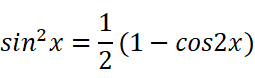
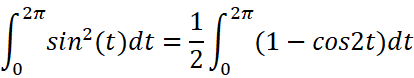
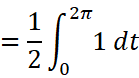
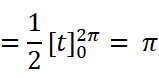
于是得到：

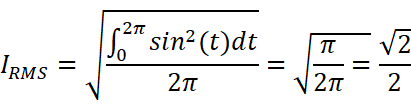
可以推广该结论。对于正弦交流电f(t)=Asin(ωx+φ)，它的有效电流（电压）就为峰值的0.707倍(即除以根号二)：

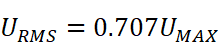
这两个公式的应用非常广泛。使用原始公式求交流电有效值是较为复杂的，传统的毫伏表、微安表、电压表、电流表、万用表都会采用这种方式，先测得交流电的最大值，然后乘以0.707得到校准平均值。而通过理论公式计算出的值叫做真有效值。

对于更复杂的交流电情形，可以考虑使用傅里叶展开来进一步计算：

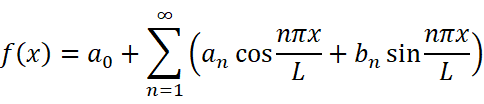
这部分本文就不进一步探讨了。