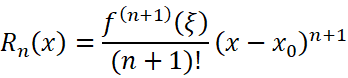
【随处可见的物理】1. 单摆的周期到底是啥？

话说十六世纪的比萨的一天，跟我差不多年龄的伽利略在礼拜时摸鱼(摸鱼是真正的第一生产力呀)，盯着教堂顶的大吊灯发呆。最开始工人不小心触动了吊灯，吊灯的摆动幅度很大，随着时间流逝，摆动幅度也就越来越小。可是，似乎无论摆动幅度是多大，吊灯来回摆动一次的时间都是相同的。于是伽利略兴奋地跑回家玩弄起了单摆。

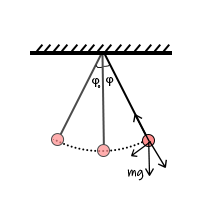
那我们也来玩弄一下吧。先画一个单摆，不妨研究它的摆动角度φ从φ0到-φ0这段半周期的过程。以φ减小的方向为正方向，请出牛顿老爷子说出他的第二定律：

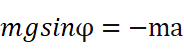
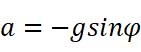
其中 a=dv/dt, v=ωl, ω=dθ/dt, 代入得到：

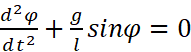
这个方程我不会解(T.T, 貌似在高中的时候也是进行到这一步)，不过回想一下高中的限定条件，在φ小于五度时近似公式

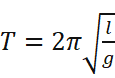
才能用。这是作了sinφ=φ的近似处理得到的结果。在φ较小时用这样的近似可以把误差控制在很小的范围内，就比如在五度时：

5^o=0.087266 rad

Sin5^o=0.087155

二者相差仅0.01%，这种误差在低精度实验时绝对是可以忽略的。

这样取近似之后可以得到这样一个可以秒杀的常系数齐次方程：

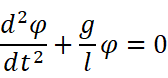
特征方程显然为

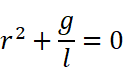
得到一对共轭复根：

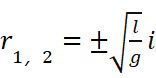
得到：

这个式子有点烦，再用辅助角公式给他化简一下：

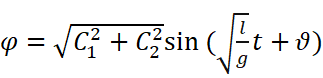
其中

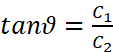
这简直和简谐运动表达式

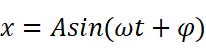
 一模一样！其实我们在近似的过程中就已经默认这个运动是简谐的了。所以很容易能写出在这种情况下周期的表达式：

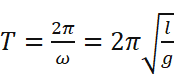
但是我们肯定不能就此收手，万一这个单摆不听话就要使劲往上摆怎么办？现在回过头去看看那个解不出来的烦人式子吧：

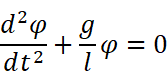
撞了南墙先回头，换种方式把这个式子重新写一遍好了：

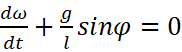
是否有机会凑出可分离变量的方程呢？想到ω可以看作是自变量为φ的函数，那就再凑一下：

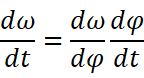
惊奇地发现

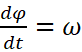
居然把t 弄消失了！于是得到一个看着舒服多了的式子：

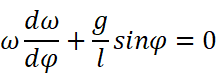
分离变量：

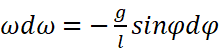
简单积个分：

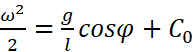
因为有初始条件，这个C₀是已知的：当φ=φ₀时ω=0，代入可知：

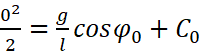
解得

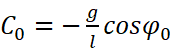
代回，即：

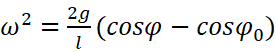
由于在设定条件时认为φ一直减小，ω作为φ的变化率，应该非正，所以取：

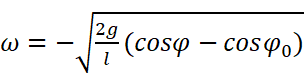
再次将ω看作关于φ的函数，然后就可以分离变量了：

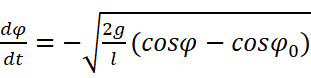
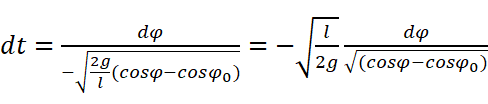
积分可得：

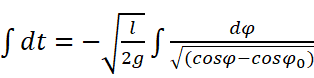
考虑在半周期内的摆动过程，可得：

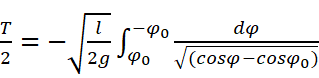
再化简一下：

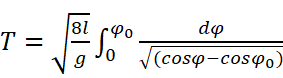
该式子为(*)式

到这里后，我的数学水平再一次阻止了我向下求解。但是我应该可以尝试去给出拟合的解。

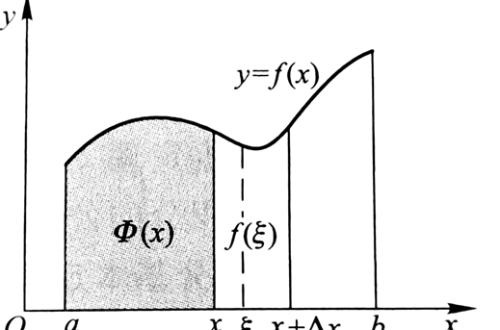
考虑麦克劳林公式：

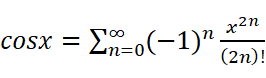
先尝试低精度的解，只保留两项，

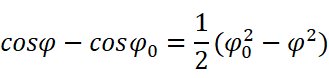
代回到(*)中得到：

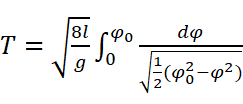
由于φ介于正负φ₀之间，可以令

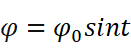
则，

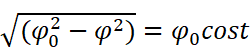
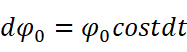
积分上下限分别变为半周期和0，则上式可以惊奇地化简为：

于是神奇地得到我们已经得到过的一个公式：

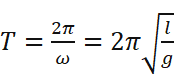
那我坚定这个思路，随着取麦克劳林展开式中项数的增多，值的拟合就会越准确。

现在取麦克劳林展开式中的三项：

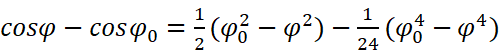
到这里计算量已经开始飙升了，不过我还是耐下性子继续往下推了推：

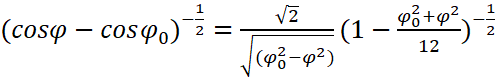
后面那一大坨东西是肯定积不出来的，于是想到用二项式定理再度近似一下：

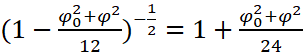
带上痛苦面具，开始往(*)里代入：

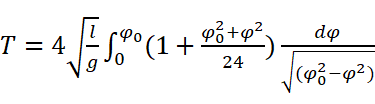
和刚才的方法一样，还是要用三角换元暴算：

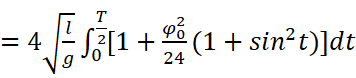
这倒是没有想象中那么难解。后面剩一点繁琐的过程就省略了吧，直接写出在这种情况下的近似解：

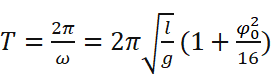
我实在没有能力找出这种解的通项公式，不过查阅资料后发现这种解法其实不是什么新颖的方法，甚至真的能找到后面每一项的参数，只不过确实没找到这种解法的通项公式。

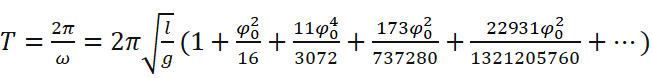
这个参数长得实在太吓人了，我很庆幸没头铁去再往下硬算一位。

值得注意的一点时，当φ0的值趋近于0时，这个公式的结果显然接近

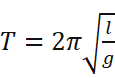
在找资料的过程里，我也顺便把之前的预留问题解决了。再回顾一下(*)，我的思路是尽可能拟合，但是它其实还能进一步往下求解：

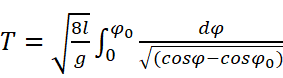
由于求解过程包含了一些我尚未学习的知识，我只能尽可能尝试把继续的思路复述一遍，希望我掌握了其中的数学工具后可以独立求解。所以下文内容并非我独立完成，特别是收尾处的部分，我几乎只有复述的能力。

首先由升幂公式

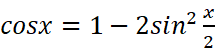
令：

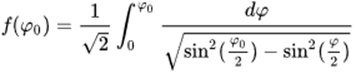
考虑这样一个变换

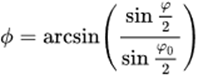
为了方便，记

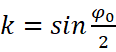
得到：

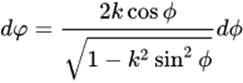
新的积分上限仍是半周期，即：

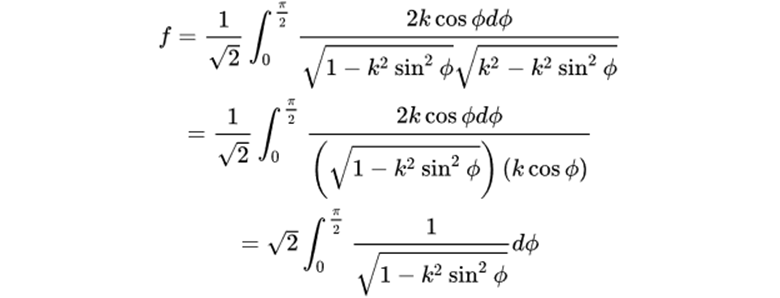
为了简化，再记：

现在(*)可以写作：

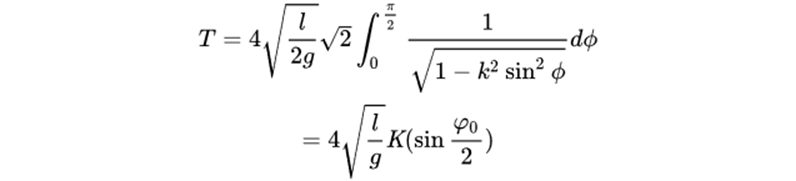
通过多项式展开的公式

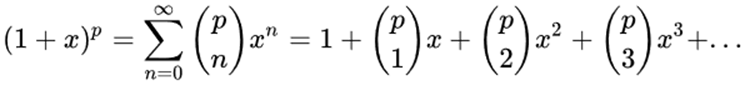
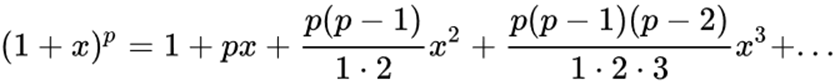
可以得到：

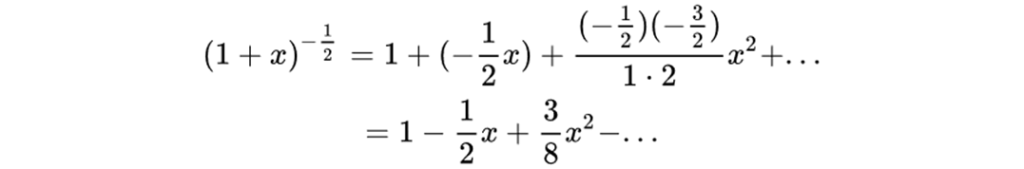
所以

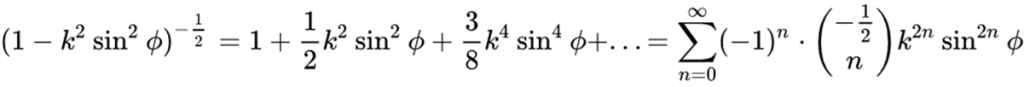
再由此公式：

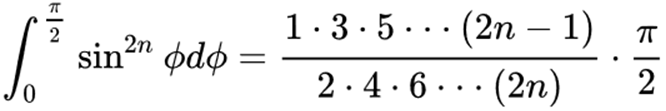
因此

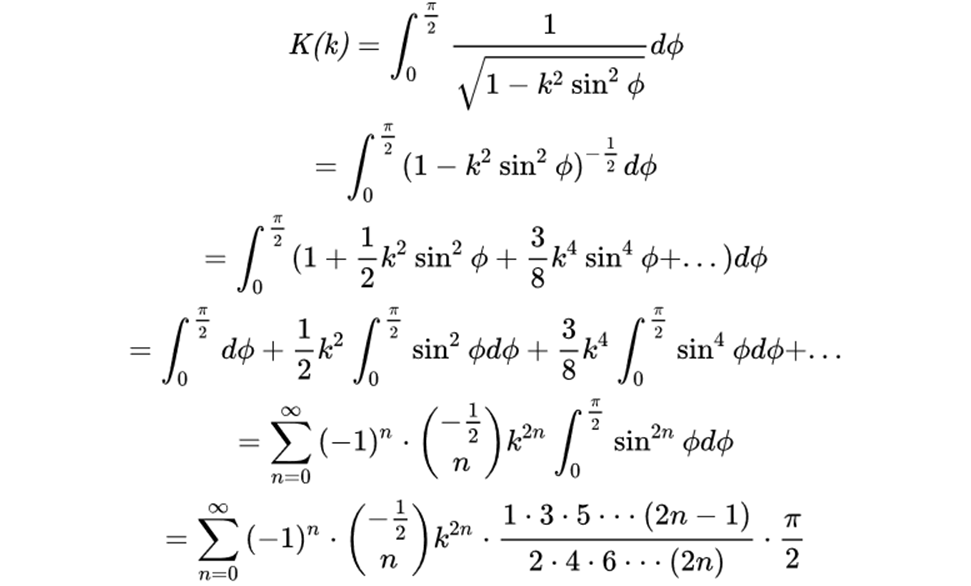
可以得到