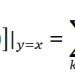【高数学习回顾】3.渐近线的爱恨情仇

高中时的数学老师特别喜欢开渐近线的玩笑：“无限接近，永不相交”，用来比喻某种爱而不得的感情状态。除此之外，时不时也能看到夜半网易云语录里出现渐近线的身影，类似“还是渐近线好，真要相交只能以后渐行渐远”，“你始终是我触碰不到的渐近线”（瞎编的，非原句）。那今天就来研究一下到底应该如何“看待”渐近线吧。

渐近线有三种：横的（水平渐近线），竖的（铅直渐近线），还有斜的（斜渐近线）。但假如你的脖子够灵活，这三者其实并没有什么区别，可以看作只是旋转了一下坐标系：

我们把水平方向作为基准吧，看看这个优美的函数：

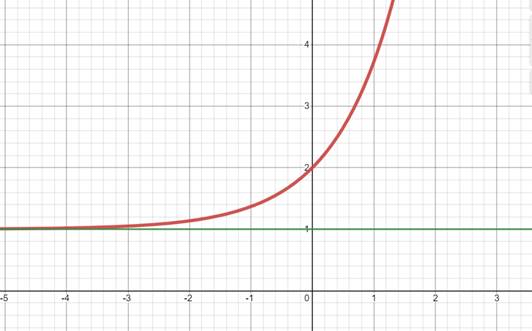
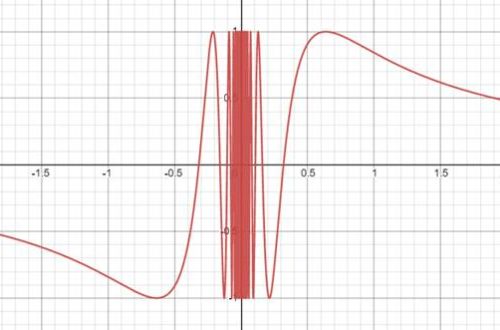
水平渐近线就这么显而易见。现在看看铅直渐近线。为了把它回到我们熟悉的领域，只需要重新建立一个旋转了九十度的坐标系，就可以把它看作水平渐近线了。看看:

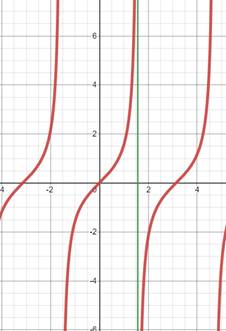
变为

斜渐近线也是同理，虽然看着复杂，重新建立一个变换过的坐标系，也可以把它重新看为水平渐近线。看看。

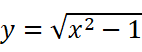
（这其实是双曲线的一部分）

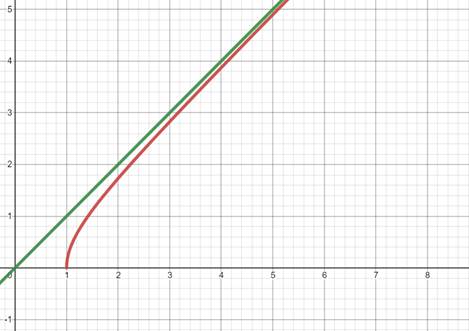
变为

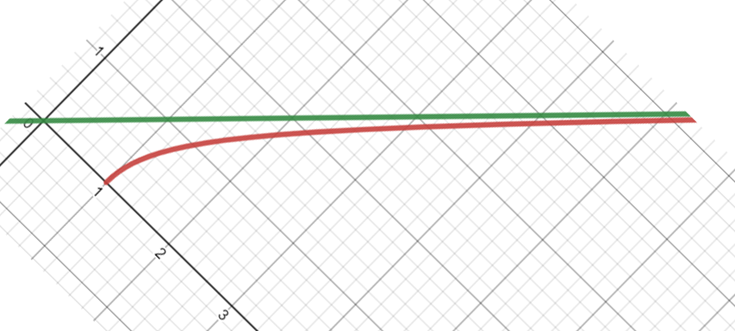
又成了水平的。基于这种思路，三种渐近线的本质都是一样的。用旋转直线的角度考虑，如果令渐近线与x轴的夹角为θ，那么：

当θ=0，即tanθ=0，即k=0时，渐近线是水平的

当θ=π/2，即tanθ→∞，即→∞或者说k不存在时，渐近线是铅直的

当0＜θ＜π/2，即tanθ=C，即k=C时，渐近线是斜率为C的渐近线

于是我们可以自然地得到计算渐近线的方法：

1.水平渐近线，典例：

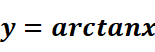
只需要

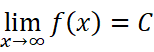
或者

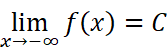
存在，则渐近线方程为：

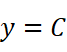
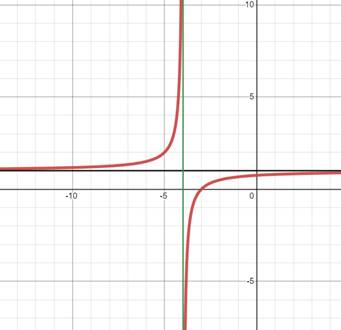
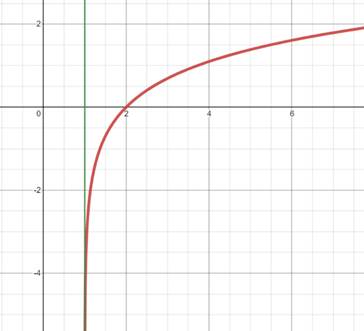
2.铅直渐近线，典例：

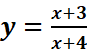
只需要

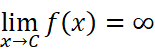
或者

则渐近线方程为：

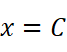
还有一个小小的困难：如何才能找到x=C这个点？根据个人经验，出现tan, log函数以及分式分母为0这些情况，可能会导致铅直渐近线出现。

3.斜渐近线，典例：

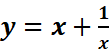
仍是随着x的增大两者越来越近。我们不妨把渐近线的方程表示出来：

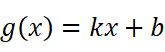
所以只需要

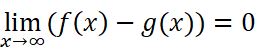
时，g(x)就是渐近线。要解出g(x)的方程是一件非常容易的事情：

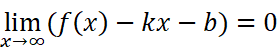
等式两边同时除以x：

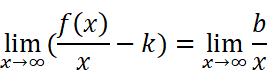
得

这样就解出k了。求b自然水到渠成：

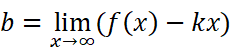
和前面一样，当x趋近于负无穷时也有可能得到渐近线。即：

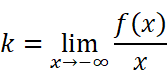
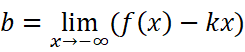
不妨用典例再来印证一下公式：

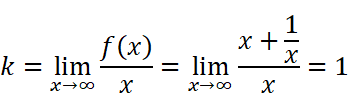
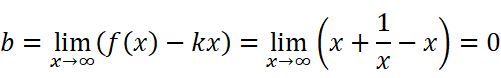
没有问题！

先不论渐近线是否是忧伤的，至少，它在坐标系里是优美的。