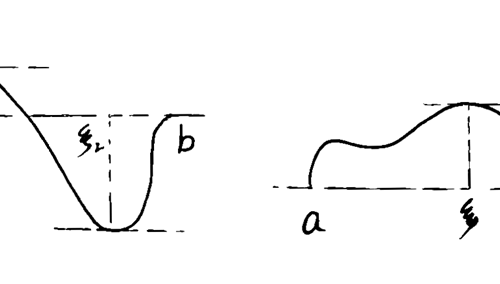
【高数学习回顾】2.函数的连续性与间断点
TIPS: 在这篇小短文里,我不打算用非常严谨的方法来研究连续、可导,还有间断点。我想从更直观的角度阐述一下自己对连续和间断的想法,所以很可能不能做到证明的严密性。
首先我们看看函数的连续是怎么定义的:
若f(x0)在点x0的某一邻域内有定义,如果
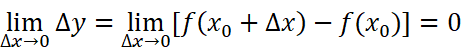
那么就称函数f(x0)在点x=x0处连续
怎么理解这个式子呢?基于定义本身直观来说,连续的函数就是:当自变量的变化足够小的时候,因变量的变化也足够小。如果自变量的某种微小的变化会导致因变量突然跳跃,或者无法定义,则这个函数被称为是不连续的函数。连续性的最根本定义其实是基于拓扑学的,这里我没有能力给出更精确的定义了。
原始定义经过不复杂的变换,我们可以得到函数在x=x0处连续的一个充分必要条件:
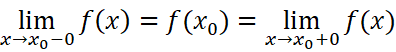
现在我们考虑一下可导与连续的关系。我有一个可能不是太严谨的想法,甚至无法判断这种想法的对错,提供在这里供大家批评。
我们知道,可导的条件是:
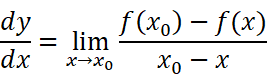
存在并且有限,则称f(x)在x0处可导。
把导数公式两边同时乘以:
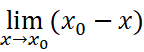
得到:
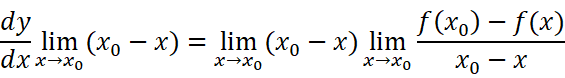
等式左边dy/dx为常量,乘以无穷小后得0。于是得到:

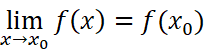
这就是连续的条件。所以可导是可以推出连续的。
至于连续不能推导出可导,是由于:不能保证
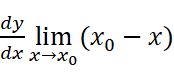
为0。
(比如当
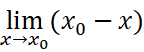
是dx/dy的高阶无穷小时,或者dx/dy根本不存在时)。
另外一个想法是:可导意味着曲线在那一点是光滑的,这显然是相对连续的一个更强的条件,很可能意味着可导一定连续,连续不一定可导。
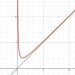
说到连续不一定可导时,一定会请出这位重量级函数:y=abs(x)
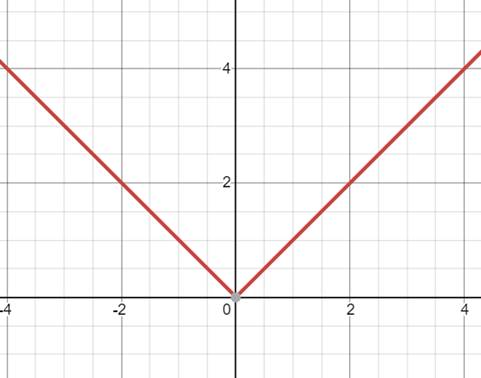
从上述的两种想法中看,这个函数是连续的,但是此时dx/dy根本不存在,函数也不是光滑的。这是一个非常经典的反例,以后要是忘了连续与可导的关系,就想一想这个优美的“V”。
现在轮到间断点了。从连续的反面思考什么是连续,可能也能加深对连续的理解。
有三种情形可能导致函数间断:
- 在x=x0没有定义
- 在x=x0有定义,但是x→x0时f(x)的极限不存在
- 虽然在x=x0有定义,而且x→x0时f(x)的极限存在,但是x→x0时f(x)的极限不等于f(x0)
根据这三个情况,我们可以把间断点分为两个大类四个小类:
- 第一类间断点:左右极限都存在。
- 可去间断点:

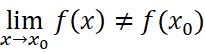
典型例子:
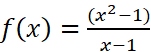
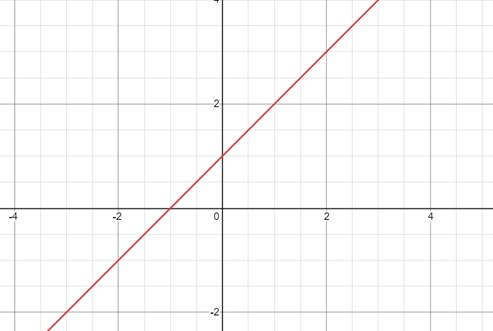
- 跳跃间断点:
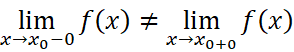
但二者都存在。典型例子:(注:阶跃函数)
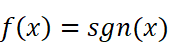
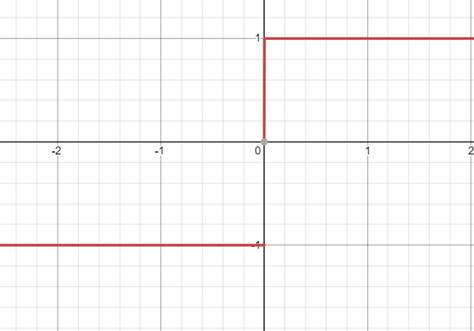
- 第二类间断点:左右极限至少有一边不存在或为无穷大。
- 无穷间断点:
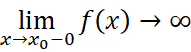
或
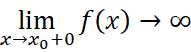
典型例子:
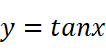
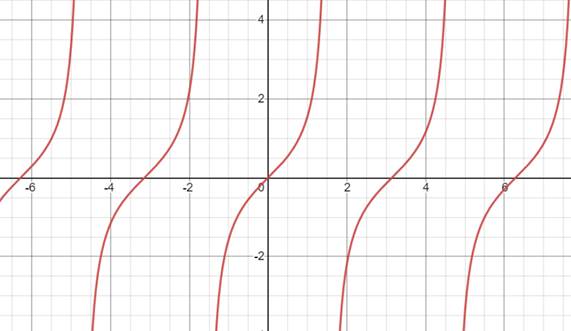
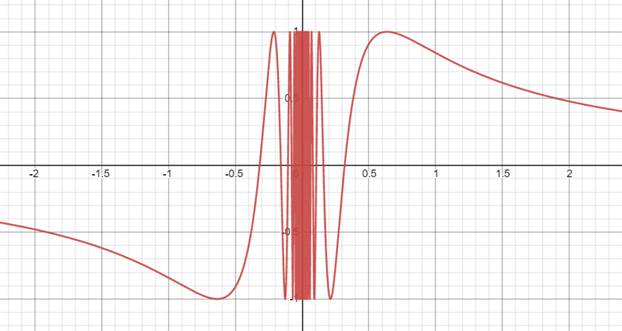
- 震荡间断点:当x→x0时,函数值在某区间内变化无限多次,极限不存在。如:
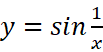

这个分类清晰我自认为很清晰。
这样看来,判断连续和间断点并不是一件复杂的事情。在我刚开始学习高数时,判断连续系列的问题经常让我痛不欲生。不过等到稍稍往后学习后,这类问题已经再也难不倒我了!不过我很怀念,彼时彼刻,我用着最最基础的数学工具思考函数连续时的样子。