前文回顾：

我们已经证明费马引理从而证明罗尔定理，再次基础上用罗尔定理证明了拉格朗日中值定理：

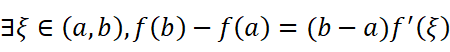
以此我们又能知道什么呢？

曲径通幽：柯西中值定理

如果不小心在使用拉格朗日中值定理时，同时写出了两个式子，你可能会发现它们有个共同的因数(b-a):

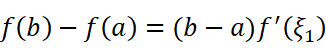
如果把两者相除消去公因式会得到什么呢？

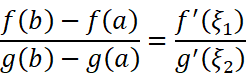
我们一定会好奇，两个ξ间会不会有什么潜在的关系呢？如果我们敢大胆地猜想：

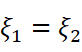
就可以得到大名鼎鼎的柯西中值定理：

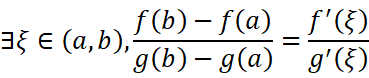
我们先来考虑一下怎样才能证明它。回想一下我们在证明拉格朗日中值定理时用到的方法，在假设柯西中值定理成立的情况下，我们可以变换出：

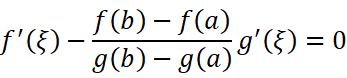
延续之前的思路，我们设出辅助函数：

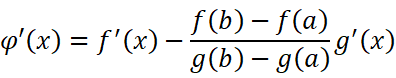
对它积分：

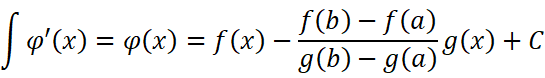
我们想找到一个C，可以使：

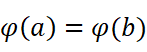
细心的读者可能会发现，这根本不需要像我们证明拉格朗日中值定理时一样东凑西凑，当C的值就为0时，很容易验证：

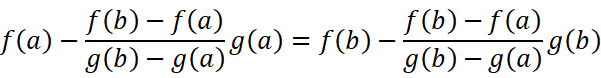
那我们就可以正式开始证明它了。让我有仪式感地写下证明这两个字：

证明：令：

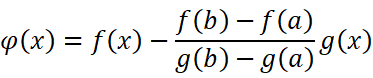
其中

由罗尔定理知：

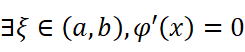
其中：

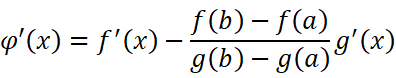
则：

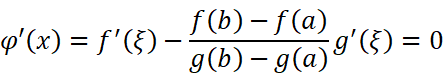
所以：

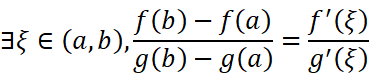
证毕。

我们观察新得到的柯西中值定理，如果令

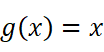
那公式就可以变形为：

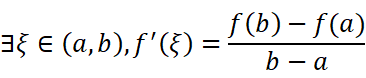
即自然地退化为拉格朗日中值定理。

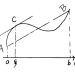
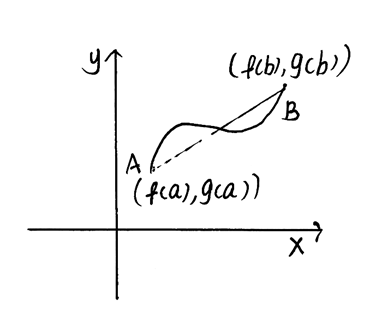
再次观察柯西中值定理，我们可能有这样的联想：如果可以把点的坐标用f(x)和g(x)表示：

那AB的斜率就可以表示为：

这样思考，我们可以得到这样一个判断：柯西中值定理是拉格朗日中值定理在参数方程形式下的表达形式。我们来证实一下：

令曲线AB的参数方程为：

则曲线上点(x,y)处切线的斜率为：

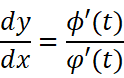
AB的斜率可以表示为：

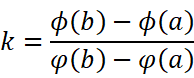
由拉格朗日中值定理可以得到：

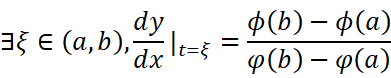
即：

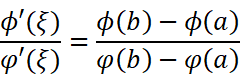
到此为止，我们已经证明了三大中值定理：罗尔定理，拉格朗日中值定理，以及柯西中值定理。那为什么这三者对建立导数应用的大厦这么重要呢？敬请见证下一节：《领略风光：洛必达法则》。