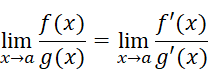
【高数学习回顾】8.筑基导数应用的大厦:洛必达定理
前文回顾:
我们已经证明了三大中值定理:由罗尔定理,到拉格朗日中值定理,最后到柯西中值定理:
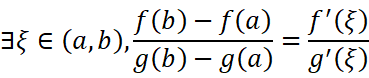
以此我们可以正式踏入倒数应用这座大厦了:
领略风光:洛必达法则
“金钱买不来知识,但是可以买来定理”
关于这个法则有个小故事:这其实是伯努利(对,就是研究流体运动的那个伯努利)发现的。洛必达是一个爱好数学的贵族,重金求伯努利给他补习数学。当时正是微积分的初创期,于是洛必达提出要购买伯努利的研究成果,并整理成了一本书:《无穷小量分析》。他在前言中提到了绝大多数成果来自伯努利和莱布尼茨,而洛必达法则正是书中的重要内容之一,洛必达自然就冠名了这个定理。
我很想述说我对一下这段历史的看法。但不会在这篇短文中。所以下面就步入正题吧:
我们曾经讨论过这样一个式子:(参考往期文章《1. 为什么要引入第一个重要极限》)
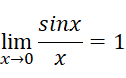
在前文的小故事中,伯努利考虑的其中一个问题就是这样:两个无穷小量能不能相除呢?表述出来就是:
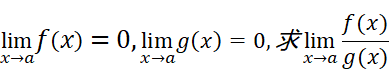
要讨论这一点,我们需要解决一个前文遗漏的问题。
铺好地板:闭区间连续,开区间可导
在《5.筑基导数应用的大厦:从费马引理和罗尔定理聊起》中,我说明了在三大中值定理中的遗留问题:
在闭区间[a,b]上连续
在开区间(a,b)上可导
我们再回顾一遍推导出这几个定理的过程。我们先证明了费马引理,通过费马引理证明了罗尔定理,通过罗尔定理证明了拉格朗日中值定理和柯西中值定理。其实,这个条件就是为了费马引理和罗尔定理预备的:
罗尔定理的证明中用到了闭区间连续函数的一个非常重要的性质:存在最大值和最小值。需要闭区间连续是为了保证端点处可以取到。而在费马引理中,又要保证f(x)在x0处可导。我们考虑到那是除端点外任意一点,所以必须要保证开区间上是可导的。具体仍见《5.筑基导数应用的大厦:从费马引理和罗尔定理聊起》。
其实,在闭区间上可导是一个更强的条件,大多数情况下,规定在闭区间[a,b]上可导就可以应用三大中值定理了,但这个条件由于被增强了,面对一些不满足条件的个例时,可能仍可以应用中值定理。典型情况是:当端点是间断点时,可以举出很多情况,如:跳跃间断点,无穷间断点,震荡间断点…
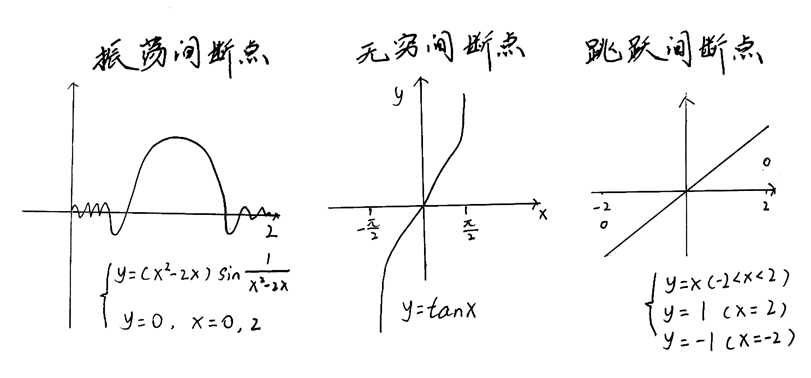
在对应的区间上,这三者都是可以使用三个中值定理的。所以为了严谨,我们应该遵守使用中值定理的这两个条件:在闭区间[a,b]上连续,在开区间(a,b)上可导。
以讨论了这个为前提,我们可以开始思考这个问题了:
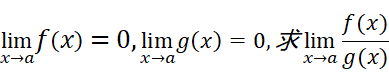
注意到f(x)与g(x)比值的极限与f(a)或g(a)无关,我们可以假定:
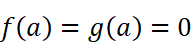
我们对待求式做个变形:
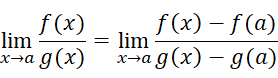
我们规定:在点a的去心邻域内f(x)和g(x)的导数都存在,这样就可以名正言顺地使用柯西中值定理了:
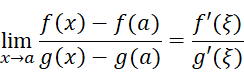
考虑到:
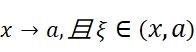
所以:
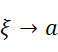
所以我们可以把待求式写为:
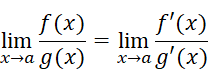
这就是著名的洛必达法则:
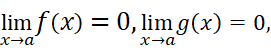
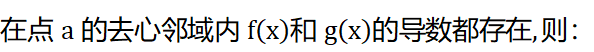
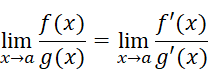
洛必达当时只考虑了x趋近于a这种情况。其实,当x趋近于无穷大时,洛必达法则仍然成立。
阅读更多:【高数学习回顾】8.筑基导数应用的大厦:洛必达定理