【高数学习回顾】12.走进定积分：积分上限的函数和牛顿-莱布尼茨公式

在学运动学时，大家肯定都遇到过这样的一个问题：如果一个车做变速运动，怎么求它所经过的路程？

我们把问题抽象一下，可以变成：已知函数f(x)，求它在某个区间与x轴围成的面积。我们应该如何解决这个问题呢？根据极限的思维，我们可以把围成的区域（可以看成曲边梯形）分成无数个小块：

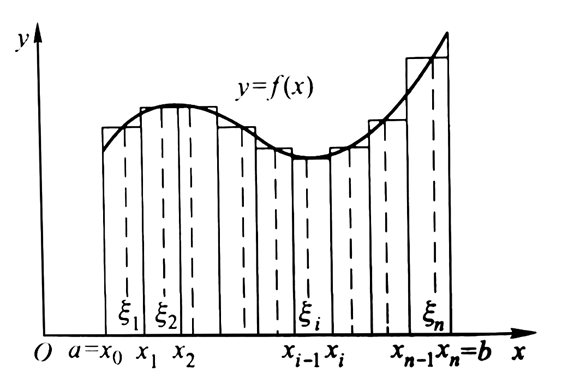
当每个小块的宽取得足够短时，就可以拟合出曲边梯形面积。把每个小长方体的宽的中点记为ξn，那它的高就可以表示为f(ξn)，于是围成区域的面积A可以表示为：

方便起见，记：

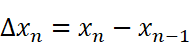
于是：

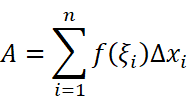
为了保证我们取到了无数个小长方体，我们需要让每个小长方体的宽都趋近于0。这只需要让宽的最大值为0就可以了。我们令：

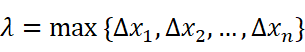
A可以严谨地表示为：

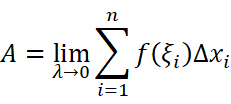
于是可以想到定义一种运算（即定积分）：

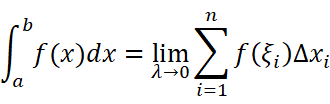
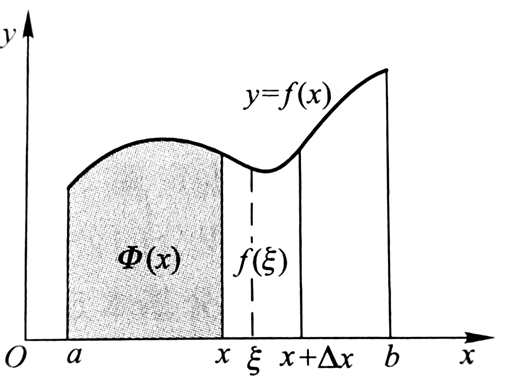
现在我们来考虑在部分区间[a,x]上的定积分：

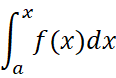
这显然是一个关于x的函数。我们可以把它记为：

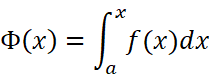
其中的x既表示定积分的上限，又表示积分变量。积分变量的记法是与定积分无关的。明确起见，我们把积分变量记作t：

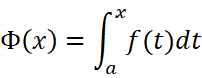
我们把这个函数叫做积分上限的函数。现在我们来研究它的性质：

它的增量是：

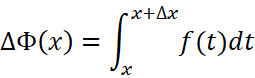
这里继续向下似乎遇到瓶颈了。我们可以先研究定积分的一个性质来解决：

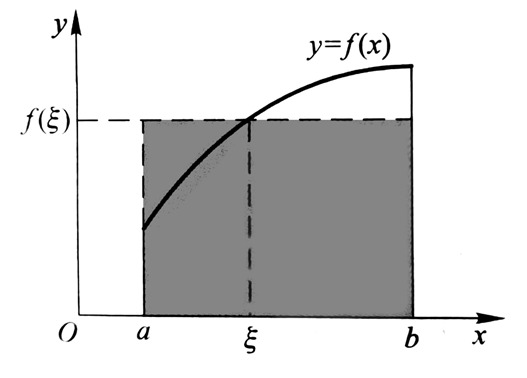
我们分别找到高M最大的长方形和高m最小的长方形，那么：

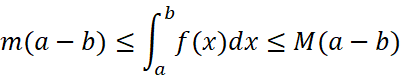
我们任取一个高为ξ的长方体，又可以得到：

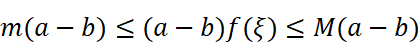
由于f(ξ)在m和M间的取值是连续的，所以一定存在一个介于a和b之间的ξ，使：

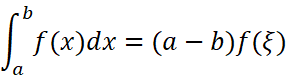
这就是定积分中值定理。

现在回到我们正在讨论的积分上限函数的增量：

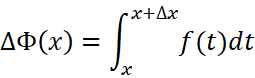
使用定积分中值定理可以得到：

其中

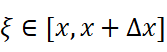
也就是：

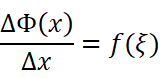
两边同时取极限：

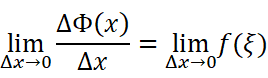
注意到：

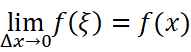
所以：

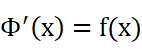
或者写做：

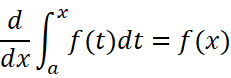
也就是说，积分上限函数是f(x)的一个原函数。

我们不难继续证明：

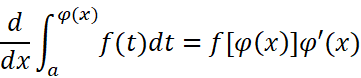
证明过程很简单。学着那些大佬的文章说一句：留给读者自证。

我们令f(x)的一个原函数为F(x)，我们知道两个原函数之差是某一个常数C：

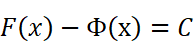
我们可以分别考虑两个端点的已知情况。注意到当x取a时：

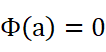
所以：

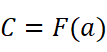
得到：

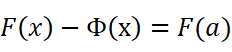
换一种表示方式：

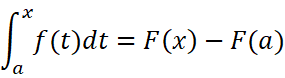
这时我们再代入x取b的情况：

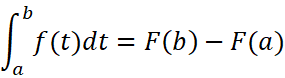
这样就得到了计算定积分的有效且简便方式，也揭示了定积分与不定积分间的关系。我们把这个公式叫做牛顿-莱布尼茨公式。为了体现它的重要性，我们也把它叫做微积分基本公式。