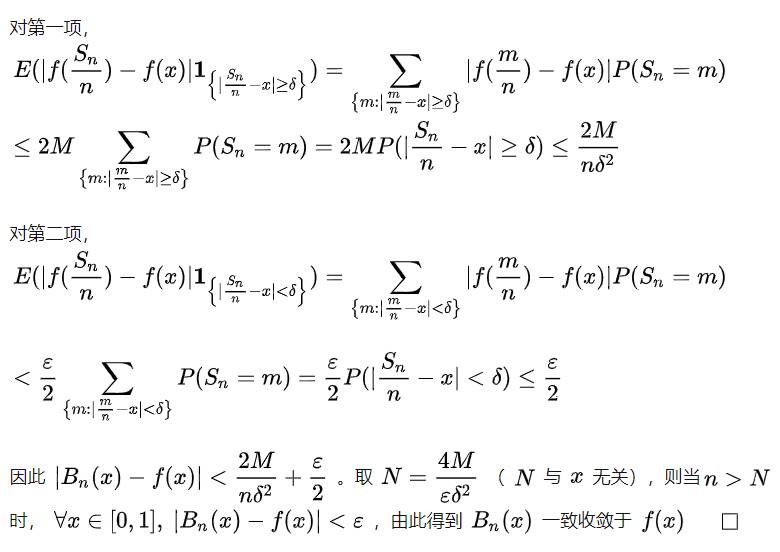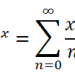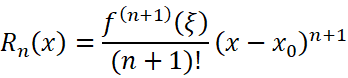
【高数学习回顾】9.筑基导数应用的大厦：泰勒公式和麦克劳林公式

对于一些较为复杂的函数（如：y=exp(x) ），为了便于研究，我们可能希望用一些简单的函数来近似表达。最常用的一种近似表达就是多项式。多项式具有一个非常优良的运算性质：只要对自变量进行有限次加减乘三种算数运算，就能求出它的函数值。

一个闭区间上的连续函数总能用多项式来近似（维尔斯特拉斯逼近定理，这是数学分析中的核心定理之一，但难度过高，不在本文想讨论的范畴之内。我将在文末摘抄一段证明。其实，在我使用的微积分教材上也直接忽略了这一点是需要证明的。而这一点恰恰是我学习泰勒公式时最疑惑的一点：凭什么可以用多项式来近似函数？初学者不妨先假设自己知道这一点，回过头来再考虑这个前提为什么成立），假设f(x)在x=a处有n阶导数，函数可以写为这样的形式：

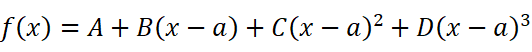
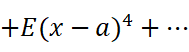
我们不停地对它求导：

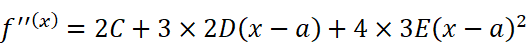
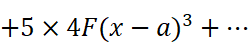
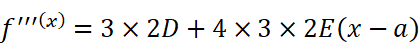
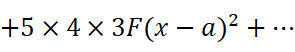
在每个等式中，分别令x=a，得到：

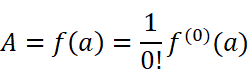
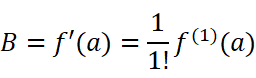
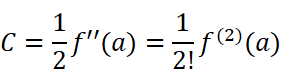
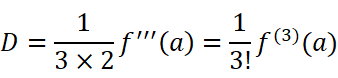
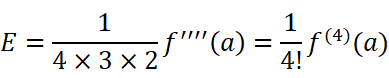
找到规律后，我们把这些系数代回原函数：

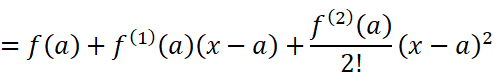
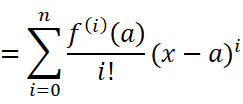
这样就接近我们今天要探讨的——泰勒公式了。接下来我们探讨一下两种不同余项的泰勒公式：

带佩亚诺余项的n阶泰勒公式：

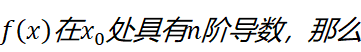
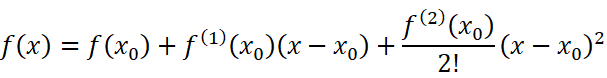
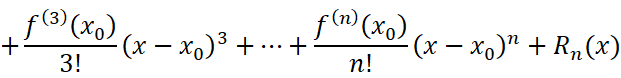
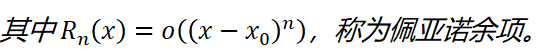
要证明佩亚诺余项是前一项的高阶无穷小，只需要证明：

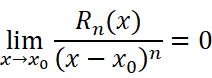
我们可以对其多次运用洛必达法则：

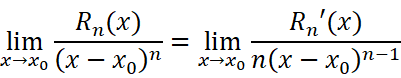
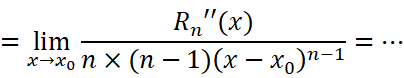
证毕。

另外一种是带拉格朗日余项的n阶泰勒公式：

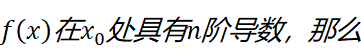
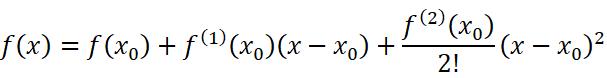
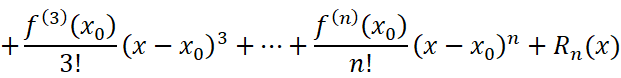
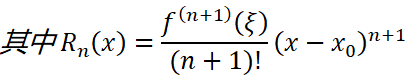
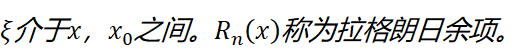
要证：

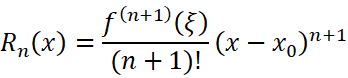
移项后即证：

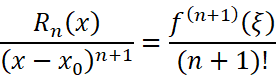
注意到：

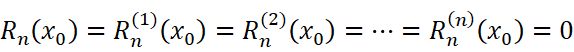
我们不难想到待证式的左边是可以构造出能使用柯西中值定理的形式的（说来奇怪，叫拉格朗日余项却要用柯西的东西）：

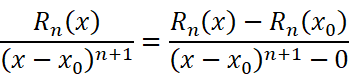
使用柯西中值定理：

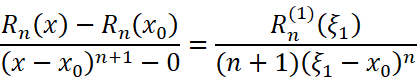
使用一次柯西中值定理后，得到的形式和之前是相似的。（是不是很奇妙！）所以我们再用一次：

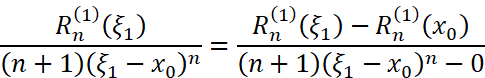
这不就能观察出来规律了嘛。我们重复使用(n+1)次柯西中值定理后可以得到：

其中

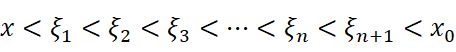
我们不难注意到：

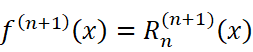
所以可以得到：

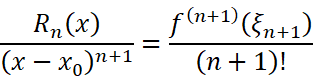
于是：

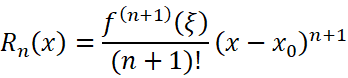
证毕。

在证明的过程中，我们肯定不止一次地想让：

那现在就来操作一下吧。先写出泰勒公式：

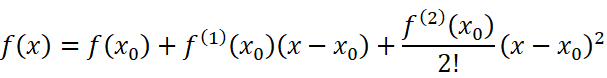
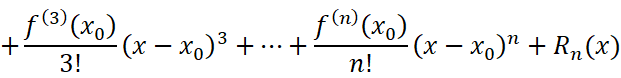
代入得：

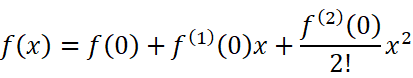
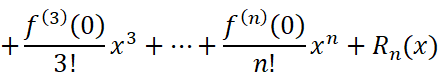
这就是麦克劳林公式。相应地代入余项可以得到带有佩亚诺余项的麦克劳林公式和带有拉格朗日余项的麦克劳林公式（怎么像绕口令一样..），麦克劳林公式在拟合函数时非常常用。在下一节我们将继续探讨麦克劳林公式。

现在是填坑时间：摘抄的维尔斯特拉斯逼近定理的证明。来自寨森Lambda-CDM. https://zhuanlan.zhihu.com/p/146181157.