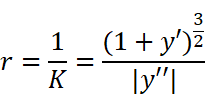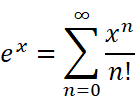【高数学习回顾】11.导数应用的实例：曲率到底是什么？

我们来看看这两个圆：

我们假设这个圆是由一条线弯曲绕成的，那在这两个圆中，哪一条线弯曲程度更大呢？

为了更直观地看出来，我们把两个圆裁剪一下：

这就很明显了。我们可以想象：一个圆半径越小，看起来就越弯曲；半径越大，看起来就越平。如果让半径趋于无穷大，圆看起来就像一条直线，就几乎不弯曲了。我们希望定义一个量来衡量几何体的弯曲程度。我们把它称为“曲率”。为了让弯曲程度越大的曲线曲率越大，越接近直线的曲线曲率越接近于0，我们把圆的半径的倒数定义为曲率。

现在我们要把这个概念推广到函数曲线上。我们可以类比一下导数的概念：

导数是把曲线的一小段当成直线求得直线的斜率

曲率就是把曲线的一小段当成圆的一部分，求得圆的半径的倒数。

通常而言，对于一般的曲线，在上面任取一点，都会有一个圆与曲线相切在这一点（即曲率圆或密切圆），即每个局部可以近似地看作一段圆弧。

我们来考虑一段圆弧MM’，补出它的曲率圆：

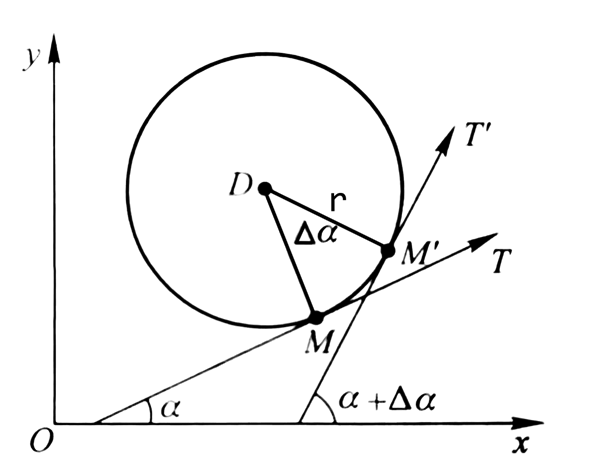
我们知道，在圆中存在这样的关系：

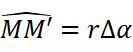
曲率K即圆的半径的倒数：

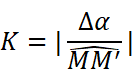
把圆弧MM’的长度记为s，考虑取极限时：

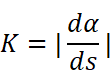
但还有一个小困难：ds指的是什么？下面马上解决：

我们观察一个过基准点M0的一段曲线：

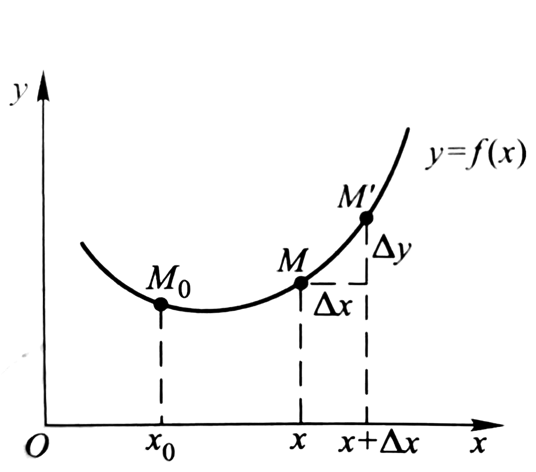
对于曲线上任意一点M，规定：

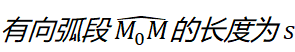
显然s是关于x的单调增函数。令M’无限接近M。则：

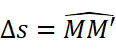
考虑到M’无限接近M，可以把它近似为线段，即：

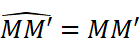
即：

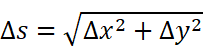
用微分形式表示：

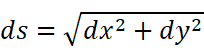
两边同时除以dx：

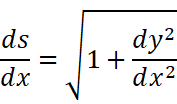
即：

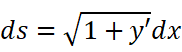
这就是弧微分。

我们之前已经得到：

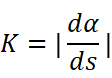
先不考虑绝对值，即：

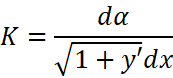
这个等式中有这样一个未知量：

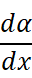
我们注意到：

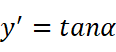
我们联想到y的二次导数可以出现这个未知量：

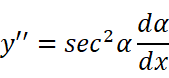
即：

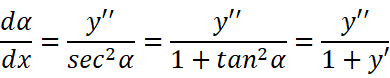
我们代回关于K的等式：

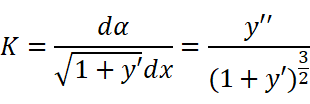
为了严谨加上绝对值，就得到了曲率的计算公式：

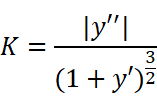
对于参数方程：

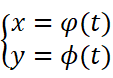
代入曲率计算公式，容易得到：

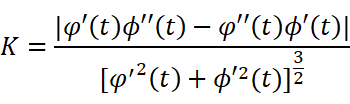
最后是前面已经提到过的，曲率圆的半径为曲率的倒数：