【高数学习回顾】10.常用的麦克劳林公式：怎么记这些鬼东西？

回顾一下麦克劳林公式：

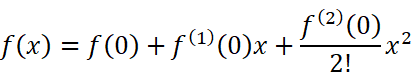
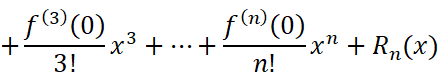
麦克劳林公式在拟合函数方面很常用。这里展示一些常用的麦克劳林公式（也就是很可能会考你的！）：

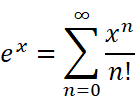
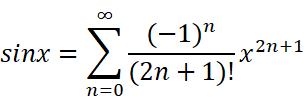
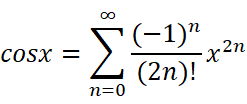
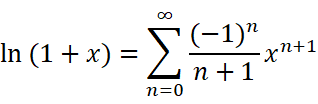
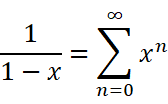
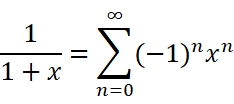
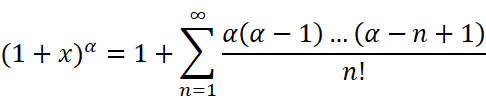
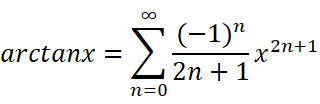
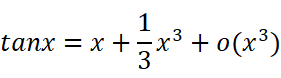
这些东西长得好吓人，打死我也不愿意去硬背它们。那有没有什么方法能迅速地记住它们呢？

从这里开始吧：

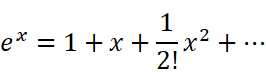
e的x次方有一个非常重要的特点：求导等于自身。也就是说，x是几次幂，它前面的阶乘就应该是几。

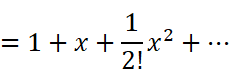
无论求几次导，最终得到的结果都是一样的。有了它，我们顺便可以推广一下结论：

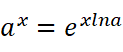
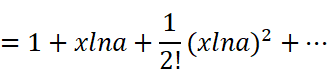
有了指数函数，现在我们来想想对数函数。

但是经过简单的推导后，我们发现对数函数很难直接用麦克劳林公式展开。那不妨先退后一步。我们可以找到这么一个非常优美的麦克劳林展开式：

它的特点是：

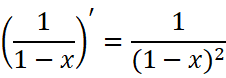
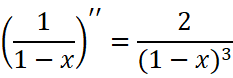
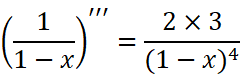
不难看出规律：

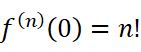
所以每一项的系数都是1。

有了这个以后，把x取相反数，自然而然可以得到：

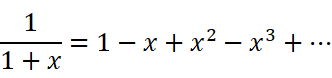
把它积分，就得到了对数函数的麦克劳林展开式：

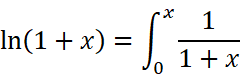
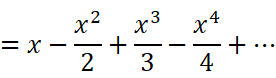
它的特点是，x是几次幂，分母就是几。（因为原本系数全为1，只是积分了一次）

如果处于一些偶然情况，式子中的(1+x)可能会很烦人。我们只需要把x换为(x-1)就能得到：

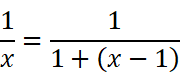
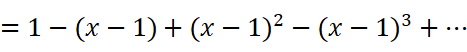
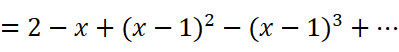
以及：

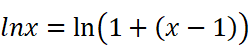
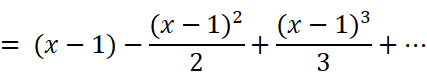
现在到了三角函数时间。

首先是最最常用的sinx，既然我们都知道了它是奇函数，只有奇数项，所以它的麦克劳林展开式是非常好记的：

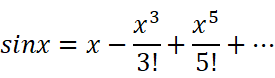
以及它只有偶数项的难兄难弟：

它的特点也是，x是几次幂，分母就是几。

这二者还有一个关系：

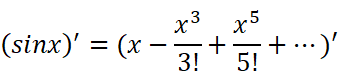
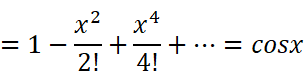
所以记住了一个也就记住了另外一个。我们顺便把tanx表示了吧：

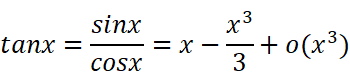
只展开到第二项是因为后面的规律比较复杂且很难看，有另外的方法去推导它。这里就不深究了。

现在我们开始考虑反三角函数。直接表示仍然不好表示，所以这个要借用之前的一个结果：

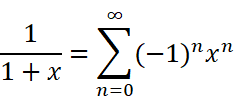
把x替换为x的平方：

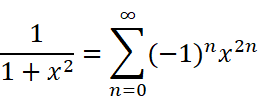
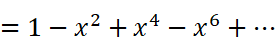
所以：

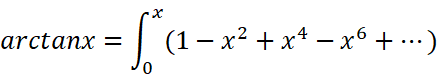
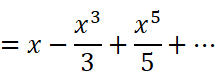
最后还剩一个孤独的式子需要记住：

虽然长得很丑，但它其实很像是二项式定理的一个推广：

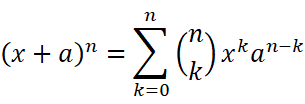
记住了二项式定理就能记住它了。